欢迎您访问52IJ教育培训网,今天小编为你分享的数学方面的学习知识是通过网络精心收集整理的:“阴影下的秘密4_...得两个月形图案AGCE和DHCF的面积之和(图中阴影部...[数学]”,注意:所整理内容不代表本站观点,如你有补充或疑问请在正文下方的评论处发表。下面是详细内容。
图案AGCE和DHCF的面积=半圆ACE面积+半圆CDF面积+三角形ACD面积-半圆ACD面积
=1/2π*(1/2AC)平方+1/2π*(1/2CD)平方+1/2AC*CD-1/2π*(1/2根号AC平方+CD平方)平方=1/2AC*CD 又因为等腰RT三角形ACD=1/2AC*CD
所以图案AGCE和DHCF的面积=等腰RT三角形ACD面积
另一种 设ac为x,ad为y,cd为z
Sace=1/2π(x/2)^2
Sabc=1/2π(y/2)^2
Scdf=1/2π(z/2)^2
因为直角三角形所以x^2+z^2=y^2
所以俩小的加起来等于那个大的
所以两个月牙的面积就等于等腰三角形的面积
其他类似问题
问题1:如图,分别以等腰Rt△ACD的边AD,AC,CD为直径画半圆.求证:所得两个月形图案AGCE和DHCF面积之和(图中阴影部分)等于Rt△ACD的面积.[数学科目]
图案AGCE和DHCF的面积=半圆ACE面积+半圆CDF面积+三角形ACD面积-半圆ACD面积
=1/2π*(1/2AC)平方+1/2π*(1/2CD)平方+1/2AC*CD-1/2π*(1/2根号AC平方+CD平方)平方=1/2AC*CD 又因为等腰RT三角形ACD=1/2AC*CD
所以图案AGCE和DHCF的面积=等腰RT三角形ACD面积
另一种 设ac为x,ad为y,cd为z
Sace=1/2π(x/2)^2
Sabc=1/2π(y/2)^2
Scdf=1/2π(z/2)^2
因为直角三角形所以x^2+z^2=y^2
所以俩小的加起来等于那个大的
所以两个月牙的面积就等于等腰三角形的面积
问题2:如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,分别以AC、BC为直径画半圆,则图中阴影部分的面积为______(结果保留π).[数学科目]
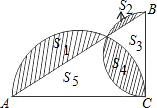
设各个部分的面积为:S1、S2、S3、S4、S5,如图所示,
∵两个半圆的面积和是:S1+S5+S4+S2+S3+S4,△ABC的面积是S3+S4+S5,阴影部分的面积是:S1+S2+S4,
∴图中阴影部分的面积为两个半圆的面积减去三角形的面积.
即阴影部分的面积=1 2
| 1 |
| 2 |
| 5 |
| 2 |
问题3:如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,分别以AC、BC为直径画半圆,则图中阴影部分的面积为______(结果保留π).[数学科目]

设各个部分的面积为:S1、S2、S3、S4、S5,如图所示,
∵两个半圆的面积和是:S1+S5+S4+S2+S3+S4,△ABC的面积是S3+S4+S5,阴影部分的面积是:S1+S2+S4,
∴图中阴影部分的面积为两个半圆的面积减去三角形的面积.
即阴影部分的面积=1 2
| 1 |
| 2 |
| 5 |
| 2 |
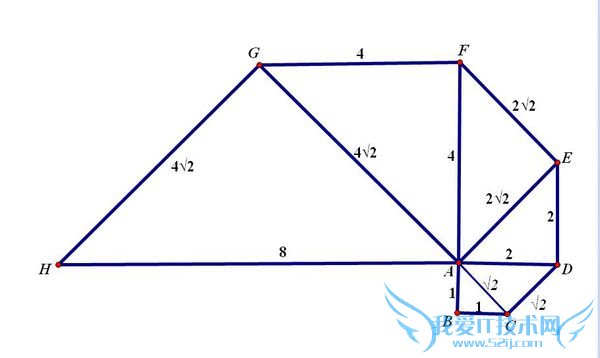
问题4:如图,已知ΔABC是边长为1的等腰直角三角形,以RtΔABC的斜边AC为直角边,画第二个等腰RtΔACD,再以RtΔACD的斜边AD为直角边,画第三个等腰RtΔADE,……如此类推.⑴求AC、AD、AE的长;⑵求第n个等腰直角[数学科目]
(1)已知ΔABC是直角边长为1的等腰直角三角形,由勾股定理可知它的斜边AC=√2
同理:
再以RtΔABC的斜边AC为直角边,画第二个等腰RtΔACD,
可知它的斜边AD=(√2)²=2
再以RtΔACD的斜边AD为直角边,画第三个等腰RtΔADE,
可知它的斜边AE=(√2)^3=2√2
(2)依次类推,第n个等腰直角三角形的斜边长=(√2)^n
问题5:如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,分别以AC、BC为直径画半圆,则图中阴影部分的面积为______(结果保留π).[数学科目]

设各个部分的面积为:S1、S2、S3、S4、S5,如图所示,
∵两个半圆的面积和是:S1+S5+S4+S2+S3+S4,△ABC的面积是S3+S4+S5,阴影部分的面积是:S1+S2+S4,
∴图中阴影部分的面积为两个半圆的面积减去三角形的面积.
即阴影部分的面积=1 2
| 1 |
| 2 |
| 5 |
| 2 |
- 评论列表(网友评论仅供网友表达个人看法,并不表明本站同意其观点或证实其描述)
-
