...第四排只有四个，其它各排有五个，怎样一笔连通不准...

精选知识

图

其他类似问题

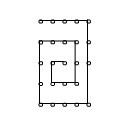
问题1：用直线连通24个圆圈,共5排,第2排为4个圈,其他为5个圈OOOOOOOOO OOOOOOOOOOOOOOO线条不能重叠,不能提笔．1排和第3排的第1个不能连．[数学科目]

O O←O O←O

↓ ↑ ↓

O←O O O

↑ ↓

O O→O O→O

↑ ↓

O→O O←O O

↑ ↓ ↑ ↓

O←O←O O←O

我疯了!我找到答案了可是为什么我答出来就不是我在下面的是一样呢?

问题2：24个点分5排对称放,第4排最后一个没有,用一条线连起来,不能斜着连,不能重复连abcdeghijklmnopqrstuvwxy用一条直线连,不能重复,不能斜着连[数学科目]

连得办法太多了:只要把缺的那个点补起来,假设这个点为F

做到一点：用一条线连起来,不能斜着连,不能重复连,且pFy三点一直线就行；

楼上只是一种,

我再给出一种：a-b-c-d-e-k-j-i-h-g-l-m-n-o-p-y-x-w-v-u-q-r-s-t

问题3：有24个球排成5排,1345是5个,第二行是4个,怎么一笔连起来,不可以斜线重复[数学科目]

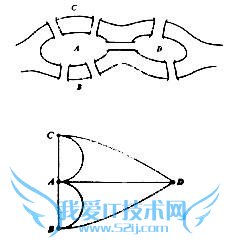
问题4：一道数学题:一个人散步,有七条桥与A.B.C.D地连接的桥,怎样才能不重复走过那七条桥[数学科目]

这个是欧拉研究过的著名的七桥问题

1736年29岁的欧拉向圣彼得堡科学院递交了《哥尼斯堡的七座桥》的论文,在解答问题的同时,开创了数学的一个新的分支-----图论与几何拓扑.也由此了数学史上的新进程.问题提出后,很多人对此很感兴趣,纷纷进行试验,但在相当长的时间里,始终未能解决.七桥问题和欧拉定理.欧拉通过对七桥问题的研究,不仅圆满地回答了哥尼斯堡居民提出的问题,而且得到并证明了更为广泛的有关一笔画的三条结论,人们通常称之为“欧拉定理”.尼斯堡七桥问题.L.欧拉用点表示岛和陆地,两点之间的连线表示连接它们的桥,将河流、小岛和桥简化为一个网络,把七桥问题化成判断连通网络能否一笔画的问题.他不仅解决了此问题,且给出了连通网络可一笔画的充要条件是它们是连通的,且奇顶点(通过此点弧的条数是奇数)的个数为0至1. 当Euler在1736年访问Konigsberg, Prussia(now Kaliningrad Russia)时,他发现当地的市民正从事一项非常有趣的消遣活动.Konigsberg城中有一条名叫Pregel的河流横经其中,这项有趣的消遣活动是在星期六作一次走过所有七座桥的散步,每座桥只能经过一次而且起点与终点必须是同一地点. Euler把每一块陆地考虑成一个点,连接两块陆地的桥以线表示 著名数学家欧拉

. 后来推论出此种走法是不可能的.他的论点是这样的,除了起点以外,每一次当一个人由一座桥进入一块陆地（或点）时,他（或她）同时也由另一座桥离开此点.所以每行经一点时,计算两座桥（或线）,从起点离开的线与最后回到始点的线亦计算两座桥,因此每一个陆地与其他陆地连接的桥数必为偶数. 七桥所成之图形中,没有一点含有偶数条数,因此上述的任务无法完成. 欧拉的这个考虑非常重要,也非常巧妙,它正表明了数学家处理实际问题的独特之处——把一个实际问题抽象成合适的“数学模型”.这种研究方法就是“数学模型方法”.这并不需要运用多么深奥的理论,但想到这一点,却是解决难题的关键. 接下来,欧拉运用网络中的一笔画定理为判断准则,很快地就判断出要一次不重复走遍哥尼斯堡的7座桥是不可能的.也就是说,多少年来,人们费脑费力寻找的那种不重复的路线,根本就不存在.一个曾难住了那么多人的问题,竟是这么一个出人意料的答案!

问题5：用1,2,3,4,5排成无重复数字的五位数,则这些数能被2整除的概率是

能被2整除

所以个位是2,4

每个数在个位出现的概率是一样的

所以概率=2/5