...则当PA+PD取最小值时，△APD中边AP上的高为( )A. 21717B. 41717...

精选知识

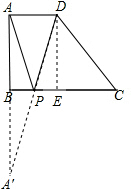过点D作DE⊥BC于E，
∵AD∥BC，AB⊥BC，
∴四边形ABED是矩形，
∴BE=AD=2，
∵BC=CD=5，
∴EC=3，
∴AB=DE=4，
延长AB到A′，使得A′B=AB，连接A′D交BC于P，此时PA+PD最小，即当P在AD的中垂线上，PA+PD取最小值，
∵B为AA′的中点，BP∥AD
∴此时BP为△AA′D的中位线，
∴BP=12

AD=1，
根据勾股定理可得AP=

AB

2

+

BP

2

=17

，
在△APD中，由面积公式可得
△APD中边AP上的高=2×4÷17

=81717

．
故选C．

其他类似问题

问题1：已知直角梯形ABCD中，AD∥BC，AB⊥BC，AD=2，BC=DC=5，点P在BC上移动，则当PA+PD取最小值时，△APD中边AP上的高为（　　）A. 21717B. 41717C. 81717D. 3[数学科目]

过点D作DE⊥BC于E，
∵AD∥BC，AB⊥BC，
∴四边形ABED是矩形，
∴BE=AD=2，
∵BC=CD=5，
∴EC=3，
∴AB=DE=4，
延长AB到A′，使得A′B=AB，连接A′D交BC于P，此时PA+PD最小，即当P在AD的中垂线上，PA+PD取最小值，
∵B为AA′的中点，BP∥AD
∴此时BP为△AA′D的中位线，
∴BP=12

AD=1，
根据勾股定理可得AP=

AB

2

+

BP

2

=17

，
在△APD中，由面积公式可得
△APD中边AP上的高=2×4÷17

=81717

．
故选C．

问题2：已知直角梯形ABCD中，AD∥BC，AB⊥BC，AD=2，BC=DC=5，点P在BC上移动，则当PA+PD取最小值时，△APD中边AP上的高为（　　）A. 21717B. 41717C. 81717D. 3[数学科目]

过点D作DE⊥BC于E，
∵AD∥BC，AB⊥BC，
∴四边形ABED是矩形，
∴BE=AD=2，
∵BC=CD=5，
∴EC=3，
∴AB=DE=4，
延长AB到A′，使得A′B=AB，连接A′D交BC于P，此时PA+PD最小，即当P在AD的中垂线上，PA+PD取最小值，
∵B为AA′的中点，BP∥AD
∴此时BP为△AA′D的中位线，
∴BP=12

AD=1，
根据勾股定理可得AP=

AB

2

+

BP

2

=17

，
在△APD中，由面积公式可得
△APD中边AP上的高=2×4÷17

=81717

．
故选C．

问题3：已知直角梯形ABCD中，AD∥BC，AB⊥BC，AD=2，BC=DC=5，点P在BC上移动，则当PA+PD取最小值时，△APD中边AP上的高为（　　）A. 21717B. 41717C. 81717D. 3[数学科目]

过点D作DE⊥BC于E，
∵AD∥BC，AB⊥BC，
∴四边形ABED是矩形，
∴BE=AD=2，
∵BC=CD=5，
∴EC=3，
∴AB=DE=4，
延长AB到A′，使得A′B=AB，连接A′D交BC于P，此时PA+PD最小，即当P在AD的中垂线上，PA+PD取最小值，
∵B为AA′的中点，BP∥AD
∴此时BP为△AA′D的中位线，
∴BP=12

AD=1，
根据勾股定理可得AP=

AB

2

+

BP

2

=17

，
在△APD中，由面积公式可得
△APD中边AP上的高=2×4÷17

=81717

．
故选C．

问题4：直角梯形ABCD中,AD‖BC,AB⊥BC,AD=2.BC=DC=5,P在BC上运动,则PA+PD取最小值时,△APD边AP上的高是多少十万火急,请快点好像是将AB延长一倍至F，然后连接DF交DP于点P，接下来就不会了，帮帮忙吧[数学科目]

过D作DE⊥BC交BC于E,则P为BE中点时PA+PD最小

容易得到DE=4=AB,故AP=根号17

则AP上的高=2*4/根号17=8/根号17

问题5：直角梯形ABCD中 AD∥BC AB⊥BC AB=12 BC=DC=13 点P在BC上移动 则当PA+PD取最小值时,△APD中边AP上高为[数学科目]

首先分析这个直角梯形

作DE垂直BC交BC于E

那么知道直角三角形CDE中,CD=13,DE=AB=12,所以CE=5,所以BE＝8,所以AD＝BE＝8.

p在bc上移动,以AD为基准,作P的镜像点F,那么PA＋PD＝FD＋DE.

在三角形PFD中,一定满足PD＋DF大于PF（三角形中两边之和大于第三边）

当P点与E点重合时候,PD＋DF＝PF,那么三角形APD就是三角形ADE.

在这个三角形中,AE的平方＝AD的平方＋ED的平方.算出AE.再有AE*高=AD*DE,算出高.

完毕.