正方形ABCD面积是264，E是AB中点，F在BC上 BC=4BF 连接...

精选知识

S(BDC)=S(ABCD)/2=132

三角形EBG∽三角形CDG

所以DG/GB=DC/EB=2

所以S(GDC)=(2/3)S(BDC)=88

S(DFB)=(1/4)S(BDC)=33

过B作BI//FD交CE于I

则IG/GH=BI/ID=1/2

IH/HC=BF/FC=1/3

所以GH/HC=2/9

所以S(GDH)=(2/11)S(GDC)=16

S(BFHG)=S(DFB)-S(GDH)=33-16=17

其他类似问题

问题1：点E、F分别是正方形ABCD边AB、BC的中点.BD、DF分别交CE于点G、H,若正方形ABCD的面积为1,则四边形BFGH的面积的等于?A1/10 B1/9 C3/25 D7/60[数学科目]

由相似易知,G是BD的三等分点,

由相似三角形也可证得,CE垂直于DF,

故BFGH=BCG-CFH=1/3BCD-1/5DCF=1/3*1/2-1/5*1/4=7/60.

问题2：正方形ABCD边长20厘米,E.F分别是AB.BC的中点,连接CE.DF相交于G点,求四边形BEGF的面积[数学科目]

易证：CE与DF垂直,（由于角CEB与角CDF互余,则角ADF与角AEC之和为180度,因此角A与角DGE之和为180度,即角DGE＝90度）

则三角形CGF与三角形CBE相似,而三角形CBE的面积为正方形面积的1/4,即100平方厘米,

因此三角形CGF的面积与三角形CBE面积比为(CF/CE)^2＝1/5,

因此三角形CGF的面积为20平方厘米

四边形BEGF面积＝三角形CBE面积－三角形CGF面积＝80平方厘米

问题3：数学题目正方形ABCD边长20厘米,E.F分别是AB.BC的中点,连接CE.DF相交于G点,求四边形BEGF的面积[数学科目]

平行于正方形ABCD中两条已有斜线作平行线,分别交于A点和B点,4条斜线形成一个斜置的井字形,将正方形分成九块,除中央一块为一小正方形外,其交点分别为GHIJ,余下8块分别为4块全等的小三角形和4块全等的小梯形.因BE=BF,故可将小三角形BJE割补到梯形BFGJ的外侧成一正方形,并与正方形GHIJ全等,即割补前的四边形BEGF面积即为小正方形GHIJ的面积.同理,井字形外面8块均可割补,两两组成4个正方形,所以大正方形共分为5个小正方形,面积=20*20/5=80cm^2.即为所求.

问题4：如图，在菱形ABCD中，已知E、F分别是边AB、BC的中点，CE、DF交于点G．若△CGF的面积为2，则菱形ABCD的面积为______．[数学科目]

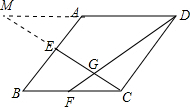如图，延长DA交CE延长线于点M，则△AME≌△BCE，
∴AM=BC，
又∵点F是BC中点，
∴CF：DM=FG：GD=1：4，
∴S_△CFG：S_△CGD=1：4，
∵△CGF的面积为2，
∴△CGD的面积为8，即可得△DFC的面积10，
∴菱形ABCD的面积为40．
故答案为：40．

问题5：26、已知:如图,在正方形ABCD中,E、F分别是AB、BC的中点,CE、DF相交于点G.26、已知：如图,在正方形ABCD中,E、F分别是AB、BC的中点,CE、DF相交于点G．求证：AD＝AG．[数学科目]

设ABCD边长为a

则:DF=√(a^2+(a/2)^2)=√5a/2

作FH//AB交CE于H

FH是△CBE的中位线,FH=BE/2=AB/4=a/4

△FHG~△DCG

FG/GD=FH/DC=1/4

FG/FD=FG/(FG+GD)=1/(1+4)=1/5

FG=FD/5

GD=FD-FG=4FD/5=2√5a/5

作AI⊥DG于I

因为∠ADI=∠DFC

所以,△ADI~△DFC

DI/FC=AD/FD=a/(√5a/2)=2√5/5

DI=FC*2√5/5=a/2*2√5/5=√5a/5

所以,DI=GD/2

所以,AI是△ADG的中线

而AI⊥DF

所以,△ADG是等腰三角形

AD=AG