2011厦门中考数学压轴题要的不是答案就是y=-x？+2m...

精选知识

E点在B点上方呀

其他类似问题

问题1：已知抛物线y=-x2+2mx-m2+2的顶点A在第一象限，过点A作AB⊥y轴于点B，C是线段AB上一点（不与点A、B重合），过点C作CD⊥x轴于点D并交抛物线于点P．（1）若点C（1，a）是线段AB的中点，求点P的坐[数学科目]

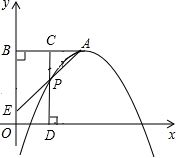（1）依题意得顶点A的坐标为（2，a），
设P（1，n）据x=-b2a

，得A点的横坐标为m，即m=2，
所以y=-x²+4x-2，把P点的坐标代入得n=1，
即P点的坐标为（1，1）
（2）把抛物线化为顶点式：y=-（x-m）²+2，
可知A（m，2），设C（n，2），
把n代入y=-（x-m）²+2得y=-（n-m）²+2，
所以P（n，-（n-m）²+2）
∵AC=CP
∴m-n=2+（m-n）²-2，
即m-n=（m-n）²，
∴m-n=0或m-n=1，
又∵C点不与端点A、B重合
∴m≠n，
即m-n=1，
则A（m，2），P（m-1，1）
由AC=CP可得BE=AB
∵OB=2
∴OE=2-m，
∴△OPE的面积S=12

（2-m）（m-1）=-12

（m-32

）²+18

，
∵边长为正数，
∴2-m＞0，m-1＞0，
∴1＜m＜2，
∴0＜S≤18

．

问题2：2011年福建省厦门市中考数学第24、25题答案[数学科目]

是这两道吗?

24、设△A1B1C1的面积是S1,△A2B2C2的面积为S2（S1＜S2）,当△A1B1C1∽△A2B2C2,且 0.3≤S1S2≤0.4时,则称△A1B1C1与△A2B2C2有一定的“全等度”．如图,已知梯形ABCD,AD∥BC,∠B=30°,∠BCD=60°,连接AC．

（1）若AD=DC,求证：△DAC与△ABC有一定的“全等度”；

（2）你认为：△DAC与△ABC有一定的“全等度”正确吗?若正确,说明理由；若不正确,请举出一个反例说明．

25、如图,矩形ABCD的边AD、AB分别与⊙O相切于点E、F, AE=3

（1）求 EF?的长；

（2）若 AD=3+5,直线MN分别交射线DA、DC于点M、N,∠DMN=60°,将直线MN沿射线DA方向平移,设点D到直线的距离为d,当时1≤d≤4,请判断直线MN与⊙O的位置关系,并说明理由．

——————————————————————————————————

24.（1）先过点D做DE⊥AC,交AC于E,利用AD∥BC,AD=DC,∠BCD=60°,可证∠DAC=∠ACD=∠ACB=30°,那么△ABC和△DAC中就有两组对应角相等,即可求它们相似．可以设DE=x,由于∠DAC=30°,所以AD=2x,AE= 3x,那么利用等腰三角形三线合一定理,可知AC=2 3x=AB,于是S△DAC：S△ABC=DA：AB=（ 2x23x）2=1：3,而0.3≤ 13≤0.4,所以两三角形有一定的全等度；

（2）不正确,举出反例进行论证其错误即可．比如可令∠ACB=40°,则∠ACD=20°,∠DAC=40°,∠BAC=110°,∠ADC=120°,显然两个三角形不相似,当然就不存在全等度了．

证明：（1）∵AD=DC

∴∠DAC=∠DCA

∵AD∥BC

∴∠DAC=∠ACB

∵∠BCD=60°

∴∠ACD=∠ACB=30°

∵∠B=30°

∴∠DAC=∠B=30°

∴△DAC∽△ABC

过点D作DE⊥AC于点E,

∵AD=DC

∴AC=2EC

在Rt△DEC中

∵∠DCA=30°,cos∠DCA= ECDC= 32

∴DC= 23EC

∴ DCAC= 13

∴ S△DECS△ADC=（ DCAC）2= 13=0.33

∵0.3 ≤S△DECS△ADC≤0.4

∴△DAC与△ABC有一定的“全等度”．

（2）△DAC与△ABC有一定的△“全等度”不正确．

反例：若

∠ACB=40°,则△DAC与△ABC不具有一定的“全等度”．

∵∠B=30°,∠BCD=60°,

∴∠BAC=110°

∵AD∥BC

∴∠D=120°

∴△DAC与△ABC不相似

∴若∠ACB=40°,则△DAC与△ABC不具有一定的“全等度”．

25.（1）连接OE、OF,利用相切证明四边形AFOE是正方形,再根据弧长公式求弧长；

（2）先求出直线M1N1与圆相切时d的值,结合1≤d≤4,划分d的范围,分类讨论．

（1）连接OE、OF,

∵矩形ABCD的边AD、AB分别与⊙O相切于点E、F,

∴∠A=90°,∠OEA=∠OFA=90°

∴四边形AFOE是正方形

∴∠EOF=90°,OE=AE= 3

∴ EF?的长= 90π×3180= 32π．

（2）如图,将直线MN沿射线DA方向平移,当其与⊙O相切时,记为M1N1,切点为R,交AD于M1,交BC于N1,

连接OM1、OR,

∵M1N1∥MN

∴∠DM1N1=∠DMN=60°

∴∠EM1N1=120°

∵MA、M1N1切⊙O于点E、R

∴∠EM1O= 12∠EM1N1=60°

在Rt△EM1O中,EM1= OEtan∠EM1O= 3tan60°=1

∴DM1=AD-AE-EM1= 3+5- 3-1=4．

过点D作DK⊥M1N1于K

在Rt△DM1K中

DK=DM1×sin∠DM1K=4×sin∠60°=2 3即d=2 3,

∴当d=2 3时,直线MN与⊙O相切,

当1≤d＜2 3时,直线MN与⊙O相离,

当直线MN平移到过圆心⊙O时,记为M1N1,点D到M1N1的距离d=DK+OR=2 3+ 3=3 3＞4,

∴当2 3＜d≤4时,MN直线与⊙O相交．

问题3：2011河南中考数学压轴题答案

23、如图,在平面直角坐标系中,直线 y=34x-32与抛物线 y=-14x2+bx+c交于A、B两点,点A在x轴上,点B的横坐标为-8．

（1）求该抛物线的解析式；

（2）点P是直线AB上方1的抛物线上一动点（不与点A、B重合）,过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E．

①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值；

②连接PA,以PA为边作图示一侧的正方形APFG．随着点P的运动,正方形的大小、位置也随之改变．当顶点F或G恰好落在y轴上时,直接写出对应的点P的坐标．

考点：二次函数综合题．专题：代数几何综合题；数形结合；待定系数法．分析：（1）利用待定系数法求出b,c即可；

（2）①根据△AOM∽△PED,得出DE：PE：PD=3：4：5,再求出PD=yP-yD求出二函数最值即可；

②当点G落在y轴上时,由△ACP≌△GOA得PC=AO=2,即 -14x2-34x+52=2,解得 x=-3±172,

所以 P1(-3+172,2),P2(-3-172,2),当点F落在y轴上时,同法可得 P3(-7+892,-7+892), P4(-7-892,-7-892)（舍去）．（1）对于 y=34x-32,当y=0,x=2．当x=-8时,y=- 152．

∴A点坐标为（2,0）,B点坐标为 (-8,-152)．

由抛物线 y=-14x2+bx+c经过A、B两点,

得 {0=-1+2b+c-152=-16-8b+c.

解得 b=-34,c=52．

∴ y=-14x2-34x+52．

（2）①设直线 y=34x-32与y轴交于点M,

当x=0时,y= -32．∴OM= 32．

∵点A的坐标为（2,0）,∴OA=2．∴AM= OA2+OM2=52．

∵OM：OA：AM=3：4：5．

由题意得,∠PDE=∠OMA,∠AOM=∠PED=90°,∴△AOM∽△PED．

∴DE：PE：PD=3：4：5．

∵点P是直线AB上方的抛物线上一动点,

∴PD=yP-yD

= (-14x2-34x+52)-(34x-32),

= -14x2-34x+4．

∴ l=125(-14x2-32x+4)

= -35x2-185x+485．

∴ l=-35(x+3)2+15．

∴x=-3时,l最大=15．

②满足题意的点P有三个,分别是 P1(-3+172,2),P2(-3-172,2),

P3(-7+892,-7+892)．