初三数学 如图，水平地面上有一面积为30πcm2的扇形AO...

精选知识

理解错了,只有滚到OA再一次垂直于地面时,圆滚过一个周长,圆心移动一个周长.也就是圆心移动的距离就是圆周滚过的距离,因为在仍一时刻,圆心相对于和地面接触的圆周（其实是个点）,都没有相对移动,圆周走的是地面的直线,圆心走的是和地面距离为半径的直线,因此圆心走过多长,圆周就在地面走多长.

注：以后学了圆周上一点的轨迹方程后可以严格证明这个问题的正确性.

其他回答

O一直平行于地面作直线运动

其他类似问题

问题1：水平地面有一面积为30πc㎡的扇形AOB,r=6cm,在OA与地面垂直并且扇形没有滑动的情况下,将扇形向右滚动至OB与地面垂直为止,则点O移动多少距离[数学科目]

设优弧AB的长是l．

根据扇形的面积公式,得

l= 2S扇形OA= 60π6=10π（cm）．

故答案为10πcm．点评：此题考查了扇形的面积公式,即S扇形= 12×弧长×圆的半径．

问题2：如图,扇形AOB的半径为5,圆心角＝45°,则扇形AOB的面积是,若在扇形AOB内部作一个正方形CDEF,使点C在OA上,点D,E在OB,点F在弧AB上,则正方形CDEF的边长为[数学科目]

弧长=45o*π*5/180o=5π/4

(2)

对照你的图形AOB按逆时针方向：

设FB=a

DB=a

DO=DC=a

半径OB=2a=5

a=5/2

问题3：如图，在扇形OAB中，半径OA=4，∠AOB=90°，BC=2AC，点P是OA上的任意一点，求PB+PC的最小值．[数学科目]

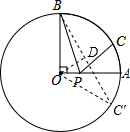先作点C关于直线OA的对称点C′，连接BC′，则BC′的长即为PB+PC的最小值，再过点O作OD⊥BC于点D，连接OC′，
∵BC

=2AC

，∠AOB=90°，
∴AC

=30°，
∴∠AOC′=30°，
∴∠BOC′=120°，
∵OD⊥BC′，OB=OC′，
∴∠BOD=60°，BD=12

BC′，
∴BD=OB?sin60°=4×32

=23

，
∴BC′=43

，即PB+PC的最小值是43

．

问题4：如图,已知扇形AOB的圆心角为90°,OA=4,C是BO的中点,以CO为半径作半圆C.求阴影部分面积S.[数学科目]

S扇形AOB=4²×90π÷360=4π

因为C是BO的中点

所以OC=OB=4÷2=2

S半圆=1²×π=π

所以S阴=S扇形AOB－S半圆=4π－π=3π

不知道答案是否准确.

也不知道你是否来得及.

希望能帮助你了.

问题5：如图，水平地面上有一面积为30πcm2的扇形AOB，半径OA=6cm，且OA与地面垂直在没有滑动的情况下，将扇形向右滚动至OB与地面垂直为止，则O点移动的距离为______．[数学科目]

设优弧AB的长是l．
根据扇形的面积公式，得
l=2

S

扇形

OA

=60π6

=10π（cm）．
故答案为10πcm．