2011年广州中考 数学 25(3)的答案25.(14分)如图7，⊙O...

精选知识

(1)∵AB是圆O直径

∴∠ACB=90°

∴ BC⊥AC

∵∠DCE是直角

∴CE⊥AC

∴B、C、E三点共线(同一平面内,经过一点有且只有一条直线垂直于已知直线 )

(2)原题求证错误.应该是OM=ON

易得：OA=OB,BM=ME

∴ OM=0.5AE

∵N是AD中点,M是BE中点,

∴ ON=0.5BD

由SAS判定方法易得

⊿BCD≌⊿ACE

∴ BD=AE

∴OM=ON(而不能得到OM=MN)

(3) ON1＝OM1仍然成立 (而不是M1N1＝OM1)

道理同(2),过程如下：

∵ OA=OB,BM=ME

∴ OM=0.5AE

∵N是AD中点,M是BE中点,

∴ ON=0.5BD

由SAS判定方法易得

⊿BCD1≌⊿ACE1

∴ BD1=AE1

∴OM1=ON1(而不能得到OM1=M1N1)

其他类似问题

问题1：2011年福建省厦门市中考数学第24、25题答案[数学科目]

是这两道吗?

24、设△A1B1C1的面积是S1,△A2B2C2的面积为S2（S1＜S2）,当△A1B1C1∽△A2B2C2,且 0.3≤S1S2≤0.4时,则称△A1B1C1与△A2B2C2有一定的“全等度”．如图,已知梯形ABCD,AD∥BC,∠B=30°,∠BCD=60°,连接AC．

（1）若AD=DC,求证：△DAC与△ABC有一定的“全等度”；

（2）你认为：△DAC与△ABC有一定的“全等度”正确吗?若正确,说明理由；若不正确,请举出一个反例说明．

25、如图,矩形ABCD的边AD、AB分别与⊙O相切于点E、F, AE=3

（1）求 EF?的长；

（2）若 AD=3+5,直线MN分别交射线DA、DC于点M、N,∠DMN=60°,将直线MN沿射线DA方向平移,设点D到直线的距离为d,当时1≤d≤4,请判断直线MN与⊙O的位置关系,并说明理由．

——————————————————————————————————

24.（1）先过点D做DE⊥AC,交AC于E,利用AD∥BC,AD=DC,∠BCD=60°,可证∠DAC=∠ACD=∠ACB=30°,那么△ABC和△DAC中就有两组对应角相等,即可求它们相似．可以设DE=x,由于∠DAC=30°,所以AD=2x,AE= 3x,那么利用等腰三角形三线合一定理,可知AC=2 3x=AB,于是S△DAC：S△ABC=DA：AB=（ 2x23x）2=1：3,而0.3≤ 13≤0.4,所以两三角形有一定的全等度；

（2）不正确,举出反例进行论证其错误即可．比如可令∠ACB=40°,则∠ACD=20°,∠DAC=40°,∠BAC=110°,∠ADC=120°,显然两个三角形不相似,当然就不存在全等度了．

证明：（1）∵AD=DC

∴∠DAC=∠DCA

∵AD∥BC

∴∠DAC=∠ACB

∵∠BCD=60°

∴∠ACD=∠ACB=30°

∵∠B=30°

∴∠DAC=∠B=30°

∴△DAC∽△ABC

过点D作DE⊥AC于点E,

∵AD=DC

∴AC=2EC

在Rt△DEC中

∵∠DCA=30°,cos∠DCA= ECDC= 32

∴DC= 23EC

∴ DCAC= 13

∴ S△DECS△ADC=（ DCAC）2= 13=0.33

∵0.3 ≤S△DECS△ADC≤0.4

∴△DAC与△ABC有一定的“全等度”．

（2）△DAC与△ABC有一定的△“全等度”不正确．

反例：若

∠ACB=40°,则△DAC与△ABC不具有一定的“全等度”．

∵∠B=30°,∠BCD=60°,

∴∠BAC=110°

∵AD∥BC

∴∠D=120°

∴△DAC与△ABC不相似

∴若∠ACB=40°,则△DAC与△ABC不具有一定的“全等度”．

25.（1）连接OE、OF,利用相切证明四边形AFOE是正方形,再根据弧长公式求弧长；

（2）先求出直线M1N1与圆相切时d的值,结合1≤d≤4,划分d的范围,分类讨论．

（1）连接OE、OF,

∵矩形ABCD的边AD、AB分别与⊙O相切于点E、F,

∴∠A=90°,∠OEA=∠OFA=90°

∴四边形AFOE是正方形

∴∠EOF=90°,OE=AE= 3

∴ EF?的长= 90π×3180= 32π．

（2）如图,将直线MN沿射线DA方向平移,当其与⊙O相切时,记为M1N1,切点为R,交AD于M1,交BC于N1,

连接OM1、OR,

∵M1N1∥MN

∴∠DM1N1=∠DMN=60°

∴∠EM1N1=120°

∵MA、M1N1切⊙O于点E、R

∴∠EM1O= 12∠EM1N1=60°

在Rt△EM1O中,EM1= OEtan∠EM1O= 3tan60°=1

∴DM1=AD-AE-EM1= 3+5- 3-1=4．

过点D作DK⊥M1N1于K

在Rt△DM1K中

DK=DM1×sin∠DM1K=4×sin∠60°=2 3即d=2 3,

∴当d=2 3时,直线MN与⊙O相切,

当1≤d＜2 3时,直线MN与⊙O相离,

当直线MN平移到过圆心⊙O时,记为M1N1,点D到M1N1的距离d=DK+OR=2 3+ 3=3 3＞4,

∴当2 3＜d≤4时,MN直线与⊙O相交．

问题2：2011年大连市中考数学25题,如图,在Rt△ABC中,∠A=90°,D为BC上一点,F为AB上一点,∠BDF=?∠ACB,BE⊥DF于E.(1)\x05若AB=AC,①∠FBE的度数为---------------.②试探究BE与DF的数量关系并证明；（2）若AB=k?

.延长be到g使be=eg连接gd交ab于h.bgh与fhd全等.1比2. 第2 同理证相似结果k 比2.不会打字

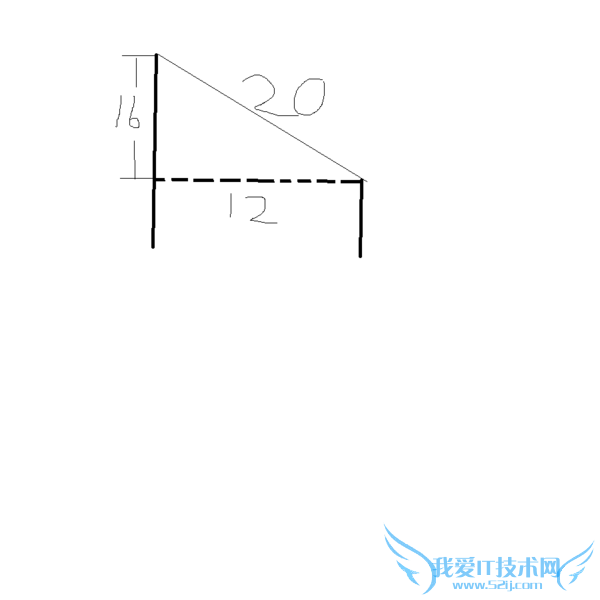
问题3：初中关于勾股定理的数学题目、请尽快在2011年3月25日的早上6：00之前回答哈,明天要交1、有一只小鸟在一棵高4m的小树最顶端捉虫子,它的伙伴在离该树12m,高20m的一棵大树的最顶端发出友好的[数学科目]

第一题,先做图,连辅助线可知,两直角边为12和16,根究勾股定理,斜边长度的平方=12*12+16*16=400 故斜边=20 飞行时间=20/4=5 故飞5秒到达大树顶.

第二题,由题意知,AO=60 AB=80 根据勾定,BO 的平方=60*60+80*80=10000 故BO=100.

子弹飞行时间=100/12.5=8 野兔奔跑时间=80/10=8 两个时间相等,所以能打中野兔.

欧了.

问题4：急``````````````````````````至少两篇字不要太少[数学科目]

今天下午,我和妈妈来到超市买东西.

当我们买完所需的东西之后,刚要离开,我看见货架上正好摆着火腿肠,于是我让妈妈买些火腿肠,妈妈同意了.可是刚走几步,我又看见货架上摆着一包一包的,同样品牌,同样重量,里面有10根,每包4.30元.到底买一包一包的呢,还是买一根一根的?我犹豫了.突然,我的脑子一转,有了,只要比较一下,哪一种合算就买哪一种.于是我开始算起来：零卖的如果买10根,每根4角,就是40角,等于4元,而整包的要4.30元,多了3毛钱,所以我决定买散装的.我把我计算的过程说给妈妈听,妈妈听了直夸我爱动脑.

标题：小学三年级---数学日记!

日期：2005-12-06 19:05:20

内容：

11月25日 星期五 晴

今天,第二节课是数学课.我们班学会了:路程=时间*速度.我们很开心!

11月28日 星期一 晴

今天,我学会了一道题,是和大家想出来的.小强每分钟走100米,小丽每分钟走150米,他们分别从甲乙两地相向而行,四分钟相遇.甲乙两地相距多少米?答案是:4*100=400(米);4*150=600(米);400+600=1000(米).你们答对了吗?