cooco_初中数学 COOCO.怎么看答案[数学]

精选知识

可圈可点网题组下有答案,点击答案即可,不行多点几次

其他回答

cooco是什么

其他类似问题

问题1：有A、B、C三把刻度尺,刻度都是从0到30个单位（单位长度不相同）,设三把尺子的0刻度和30刻度外,到尺子边沿的长度忽略不计,现用其中一把尺子度量另外两把尺子的长度.已知用C尺度量,得A尺[数学科目]

设A尺的单位为a,B尺的单位为b,C尺的单位为c,那么

30a-30b=6c

30b-30c=10a

两者相加最后得5a=9c

所以A的单位为9,C的单位为5,解出B的单位为8,A-C=30×9-30×5=120

120÷8=15

毕业很多年了,叙述有错的地方请见谅.

2楼,6和10不能相加,它俩不是一个单位的

问题2：初中数学解答题!要写过程1、根据条件求二次函数的解析式（1）抛物线过（－1,－22）,（0,－8）,（2,8）三点；（2）抛物线过（－1,0）,（3,0）,（1,－5）三点；（3）二次函数的图象经过点（－[数学科目]

(1)设抛物线方程为y=ax^2+bx+c

分别将三点（－1,－22）,（0,－8）,（2,8）代入得

a-b+c=-22

c=-8

4a+2b+c=8

解方程组得a=-2,b=12,c=-8

既抛物线方程为y=-2x^2+12x-8

(2)设抛物线方程为y=ax^2+bx+c

分别将三点（－1,0）,（3,0）,（1,－5）代入得

a-b+c=0

9a+3b+c=0

a+b+c=-5

解方程组得a=5/4,b=-5/2,c=-15/4

既抛物线方程为y=5/4x^2-5/2x-15/4

(3)设抛物线方程为y=ax^2+bx+c,其过点－1,0）,（3,0）,说明方程ax^2+bx+c有两个解,x1+x2=-b/a=2,抛物线的对称轴为-b/(2a)=1,对称点对应其极值

分别将三点（－1,0）,（3,0）,（1,3）代入得

a-b+c=0

9a+3b+c=0

a*1+b*1+c=3

解方程组得a=-3/4,b=3/2,c=9/4

既抛物线方程为y=3/4x^2+3/2x+9/4

(4)设抛物线方程为y=ax^2+bx+c,抛物线的对称轴为x=-b/(2a)=1,

分别将三点（－1,0）,（0,6）,代入得

a-b+c=0

c=6

-b/(2a)=1

解方程组得a=-2,b=4,c=6

既抛物线方程为y=-2x^2+4x+6

问题3：1.一只船顺水航线速度为50千米/时,逆水航行速度为40千米/时,则水流速度为______2.小明在公路上行走,速度是每小时6千米,一辆车身长20米的汽车从背后驰来,并从小明身旁驶过来,驶过小明身旁的

1.水流速度为5千米/时

2.汽车的行驶速度是每小时54千米

3.该种商品降价前的售价6000元

4.他们的运动速度分别为3:2

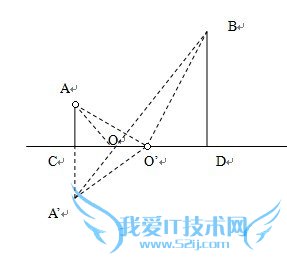
问题4：初中数学题 http://czsx.cooco.net.cn/testdetail/6143/ 我想问为什么这样费用是最少的[数学科目]

要说明这个问题就要明白为什么,答案中所选的点o是使得AO+BO距离最小的

那么我就来证明这一点

首先图中一开始作的点A'实际上是A关于CD的对称点,这一点应该很容易理解

那么我们假设CD上有另一点O‘ 是不同于O的一个点,

跟据对称性我们可以得出结论,AO’+BO'=A'O'+BO'

那么跟据两点之间直线最短,就能得出结论A‘O+BO<A'O'+BO'

也就是说AO+BO<AO’+BO'

也就是点o是使得AO+BO距离最小的点

问题5：AB是圆O的直径,AP是圆O的切线,A是切点 BP与圆O交于点C D为AP的中点 求直线CD是圆O的切线 （即证明∠OCD＝90°）[数学科目]

证明：连接AC、OC.

∵AB是直径,点C在⊙O上.

∴∠ACB＝90°

AC⊥PB

在Rt⊿ACP中.点D是PA的中点.

∴AD＝PD＝CD

则：∠PCD＝∠P,∠ACD＝∠DAC.

∵OA＝OC

∴∠OAC＝∠OCA

∵AC⊥PB,PA是⊙O的切线

∴∠PAB＝90°

∠OAC＝∠P

∴∠PCD＋∠ACD＝∠OCA＋∠ACD＝90°

即：∠OCD＝90°

∴CD是⊙O的切线.