欢迎您访问52IJ教育培训网,今天小编为你分享的数学方面的学习知识是通过网络精心收集整理的:“如图 抛物线y_如图,一条抛物线y=ax2+bx(a≠0)的顶点坐标为(2,83),...[数学]”,注意:所整理内容不代表本站观点,如你有补充或疑问请在正文下方的评论处发表。下面是详细内容。
(1)∵抛物线y=ax2+bx(a≠0)的顶点坐标为(2,8 3
∴设顶点式形式为y=a(x-2)2+
| 8 |
| 3 |
则a(0-2)2+
| 8 |
| 3 |
解得a=-
| 2 |
| 3 |
所以,y=-
| 2 |
| 3 |
| 8 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
故抛物线解析式为y=-
| 2 |
| 3 |
| 8 |
| 3 |
(2)设正方形ABCD的边长为2m,
∵抛物线对称轴为直线x=2,AB落在x轴的正半轴上,顶点C、D在这条抛物线上,
∴点C的坐标为(2+m,2m),
∴-
| 2 |
| 3 |
| 8 |
| 3 |
整理得,m2+3m-4=0,
解得m1=1,m2=-4(舍去).
所以正方形ABCD的边长为2m=2×1=2.
其他类似问题
问题1:如图,抛物线y=ax²+bx+4(a不等于0),经过等腰梯形ABCD的四个顶点,已知DC∥X轴买点A、B在X轴上,点C在Y轴上,且AC=根号17,顶点在函数y=x²-4x的对称轴上1)求A,B,C,D的坐标2)求抛物线解析式3)[数学科目]
1) 抛物线y=x^2-4x的对称轴x=2,抛物线交y轴只有一点C(0,4),题有问题角A与角C是对角,设A(x,0),C(0,y) x^2+y^2=17 x=-1或1,因为对称轴x=2,A(1,0),C(0,4),B(3,0),D(4,4) 或A(-1,0),C(0,4),B(5,0),D(4,4) 2)由题目得,y=x^2-4x+8或y=x^2+2x+5 3)F到对称轴E距离为CD的长度,是4.F(6,20),C(6,53),B(2,13),(2,4)
问题2:正方形ABCD的顶点B、C在x轴的正半轴上,A、D在抛物线y=-2/3x²+8/3x上,求正方形ABCD的边长.[数学科目]
设正方形的边长为a(a>0),A点横坐标为x,那么很容易知道A的坐标为A(x,a),
D的坐标为D(x+a,a),把这两点代入抛物线方程,可得到
-(2/3)x²+(8/3)x=a,-(2/3)(x+a)²+(8/3)(x+a)=a,解方程组即可求出a,不过这种方法有点麻烦
可以用下面方法简单一些,线段AD中点在抛物线对称轴x=2上,所以有[a+(x+a)]/2=2,
解得x=4-2a,代入-(2/3)x²+(8/3)x=a,消去x,也可以求出a,这个方法解一个二次方程即可.
问题3:如图二次函数y=-mx2+4m图象的顶点坐标为(0,2),矩形ABCD的顶点B,C在x轴上,A,D在抛物线上,矩形ABCD在抛物线与x轴所围成的区域内. (1)求二次函数的解析式.(2)设点A的坐标为(x,y[数学科目]
(1)∵二次函数y=-mx2+4m的顶点坐标为(0,2),
∴4m=2,
即m=1 2
∴抛物线的解析式为:y=-
| 1 |
| 2 |
(2)∵A点在x轴的负方向上坐标为(x,y),四边形ABCD为矩形,BC在x轴上,
∴AD∥x轴,
又因为抛物线关于y轴对称,
所以D、C点关于y轴分别与A、B对称.
所以AD的长为-2x,AB长为y,
所以周长p=2y-4x=2(-
| 1 |
| 2 |
∵A在抛物线上,且ABCD组成矩形,
∴x<2,
∵四边形ABCD为矩形,
∴y>0,
即x>-2.
所以p=-(x+2)2+8=-x2-4x+4,其中-2<x<0.
问题4:已知,正方形ABCD的两个顶点在抛物线y=x^2+c上,另两点C,D在X轴上,正方形ABCD的面积等于4,求抛物线的解析式![数学科目]
正方形的面积为4
所以BC=2,OC=1
所以点B的坐标为(1,-2)
将(1,-2)代入
可得c=-3
所以解析式为y=x²-3
问题5:如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,-1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不[数学科目]
(1)∵抛物线的顶点为Q(2,-1),
∴设抛物线的解析式为y=a(x-2)2-1,
将C(0,3)代入上式,得:
3=a(0-2)2-1,a=1;
∴y=(x-2)2-1,即y=x2-4x+3;
(2)分两种情况:
①当点P1为直角顶点时,点P1与点B重合;
令y=0,得x2-4x+3=0,解得x1=1,x2=3;
∵点A在点B的右边,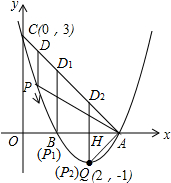
∴B(1,0),A(3,0);
∴P1(1,0);
②当点A为△AP2D2的直角顶点时;
∵OA=OC,∠AOC=90°,
∴∠OAD2=45°;
当∠D2AP2=90°时,∠OAP2=45°,
∴AO平分∠D2AP2;
又∵P2D2∥y轴,
∴P2D2⊥AO,
∴P2、D2关于x轴对称;
设直线AC的函数关系式为y=kx+b(k≠0).
将A(3,0),C(0,3)代入上式得:3k+b=0 b=3
解得
|
∴y=-x+3;
设D2(x,-x+3),P2(x,x2-4x+3),
则有:(-x+3)+(x2-4x+3)=0,
即x2-5x+6=0;
解得x1=2,x2=3(舍去);
∴当x=2时,y=x2-4x+3=22-4×2+3=-1;
∴P2的坐标为P2(2,-1)(即为抛物线顶点).
∴P点坐标为P1(1,0),P2(2,-1);
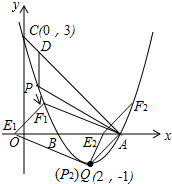
(3)由(2)知,当P点的坐标为P1(1,0)时,不能构成平行四边形;
当点P的坐标为P2(2,-1)(即顶点Q)时,
平移直线AP交x轴于点E,交抛物线于F;
∵P(2,-1),
∴可设F(x,1);
∴x2-4x+3=1,
解得x1=2-
| 2 |
| 2 |
∴符合条件的F点有两个,
即F1(2-
| 2 |
| 2 |
- 评论列表(网友评论仅供网友表达个人看法,并不表明本站同意其观点或证实其描述)
-
