如图，抛物线y=-12x2+52x-2与x轴相交于点A、B，与y轴相...

精选知识

（1）在抛物线y=-12

x²+52

x-2上，
令y=0时，即-12

x²+52

x-2=0，
得x₁=1，x₂=4
令x=0时，y=-2
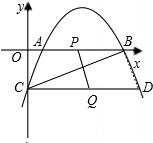
∴A（1，0），B（4，0），C（0，-2），
S_△ABC=3．
（2）设经过t秒后，PQ=AC．
∵A（1，0）、B（4，0）
∴AB=3
∴BP=3-t
∵CD∥x轴，点C（0，-2）
∴点D的纵坐标为-2
∵点D在抛物线y=-12

x²+52

x-2上
∴D（5，-2）
∴CD=5
∴CQ=5-1.5t
①当AP=CQ，即四边形APQC是平行四边形时，PQ=AC．
t=5-1.5t，t=2；
②连接BD，当DQ=BP，即四边形PBDQ是平行四边形时，PQ=BD=AC．
3-t=1.5t，t=65

．

其他类似问题

问题1：如图,抛物线y=x^2-2x-3与x轴交A.B两点速求：如图,抛物线y=x^-2x-3与x轴交A.B两点(A在B左边),直线l与抛物线交于A.C两点,其中C点的横坐标为20 - 提问时间2007-12-2 13:42 问题为何被关闭1.求AB两点的坐标[数学科目]

1 y=(x-1)^2-4 则 A （-1,0） B（3,0） C（2,-3） AC解析式为y=-x-1

2 PE=P点纵坐标-E点纵坐标=-x-1-x^2+2x+3=-(x-1/2)^2+9/4 x属于[-1,2]因为可取1/2 所以最大值9/4

3 分析A F2点关系 要么四边形邻点 要么对点 （1）若为邻点 必有AF//GC 因为AF为X轴 所以GC//x轴 再加上G为抛物线上的点 所以容易得G为（0,-3）要想四边形是平行四边形 FG和AC必互相平分 即有公共中心 容易得F=（1,0）

（2）若为对点 且想四边形是平行四边形 那么G C2点必关于AF对称 所以G点纵坐标必为3 则G为（1+根号7,3）或者（1-根号7,3） 来求2点 对应不同的F 只需满足AF和CG有公共的中心 具体解多少不求了 方法跟（1）雷同

问题2：如图,抛物线y=1/2x2+bx+c与y轴交于点C（0,-4）,与x轴交于点A,B,且B点的坐标为（2,0）（1）求该抛物线的表达式 （2）若点P是AB上的一动点,过点P作PE//AC,交BC于点E,连结CP,求△PCE面积的最大值[数学科目]

问题3：如图，已知抛物线y＝12x2+bx+c与x轴交于A （-4，0）和B（1，0）两点，与y轴交于C点． （1）求此抛物线的解析式；（2）设E是线段AB上的动点，作EF∥AC交BC于F，连接CE，当△CEF的面积是△BEF面积[数学科目]

（1）∵抛物线y＝12

x

2

+bx+c

与x轴交于A （-4，0）和B（1，0）两点，
∴12×16?4b+c＝012×1+b+c＝0

，
解得：b＝32c＝?2

，
故此抛物线的解析式为：y=12

x²+32

x-2；
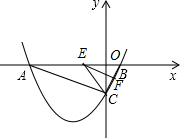（2）由（1）知：C（0，-2）；
∵S_△CEF=2S_△BEF，
∴CF=2BF，BC=3BF；
∵EF∥AC，
∴BEAB

=BFBC

=13

，
∵AB=5，
∴BE=53

，
∴OE=BE-OB=23

，
∴点E的坐标为：（-23

，0）．

问题4：如图,抛物线y＝-x的平方＋2x＋3与x轴相交于A,B两点,与y轴相交于点C,顶点为D [数学科目]

最佳吧~~

问题5：如图,抛物线y=-1/2x^2+根号2/2x+2与x轴交于A、B两点,与y轴交于C点.（1）求A、B、C三点的坐标如图,抛物线y=-1/2x^2+根号2/2x+2与x轴交于A、B两点,与y轴交于C点.（1）求A、B、C三点的坐标（2）证明△ABC[数学科目]

1、令x=0 求得y=2

令y=0求得 x=√2 或-2√2

所以A（-2√2,0） B（√2,0 ）C（0,2）

2、根据两点之间的距离公式AB²=18 AC²=12 BC²=6

所以AC²+BC²=AB² 三角形ABC是直角三角形

3、找B点关于抛物线的对称轴对称的点即可

抛物线的对称轴是x=√2/2

所以P点的坐标就是(√2,2)了