欢迎您访问52IJ教育培训网,今天小编为你分享的数学方面的学习知识是通过网络精心收集整理的:“安小宁_(x→∞,y→∞)lim(x^2+y^2)÷(arctanx+(x-y)^2)求极限[数学]”,注意:所整理内容不代表本站观点,如你有补充或疑问请在正文下方的评论处发表。下面是详细内容。

其他类似问题
问题1:lim(x→∞)arctanx/x的极限[数学科目]
lim(x→∞)arctanx/x
=(½π)/∞
=0
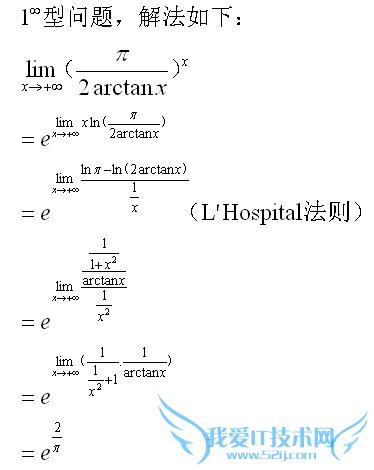
问题2:求极限lim(2/π*arctanx)^x x→∞
如图

问题3:求极限 当x趋向+∞时,lim(π/2·arctanx)^x不好意思 括号里是 2/π乘以arctanx[数学科目]
看图片:
问题4:求极限lim(2/π arctanx)^x 其中x趋向于正无穷大[数学科目]
设y=[(2/π)arctanx]^x
则:lny=xln[(2/π)arctanx]=x[ln(2/π)+lnarctanx]
lim[x→+∞] lny
=lim[x→+∞] x[ln(2/π)+lnarctanx]
=lim[x→+∞] [ln(2/π)+lnarctanx]/x?1
洛必达法则
=lim[x→+∞] -{1/[(1+x2)arctanx]} / x?2
=lim[x→+∞] -x2/[(1+x2)arctanx]
=lim[x→+∞] -1/[(1/x2 + 1)arctanx]
=-2/π
希望可以帮到你,如果解决了问题,请点下面的"选为满意回答"按钮.
问题5:求极限:lim(x→+∞)(2/π arctanx)x[数学科目]
此题打错了,原题应该是:求极限:lim(x→+∞)(2/π arctanx)^x
解法一:原式=e^{lim(x->+∞)[x(ln(arctanx)+ln(2/π))]} (应用初等函数的连续性和对数性质)
=e^{lim(x->+∞)[(ln(arctanx)+ln(2/π))/(1/x)]}
=e^{lim(x->+∞)[((1/arctanx)(1/(1+x2)))/(-1/x2)]} (0/0型极限,应用罗比达法则)
=e^{lim(x->+∞)[(1/arctanx)(-1/(1+1/x2))]}
=e^[(1/(π/2))(-1/(1+0))]
=e^(-2/π);
解法二:原式=lim(x->+∞){[(1+(2arctanx-π)/π)^(π/(2arctanx-π))]^[x(2arctanx-π)/π]}
={lim(x->+∞)[(1+(2arctanx-π)/π)^(π/(2arctanx-π))]}^{lim(x->+∞)[x(2arctanx-π)/π]}
=e^{lim(x->+∞)[x(2arctanx-π)/π]} (应用重要极限lim(z->0)[(1+z)^(1/z)]=e)
=e^{lim(x->+∞)[(2arctanx-π)/(π/x)]}
=e^{lim(x->+∞)[(2/(1+x2))/(-π/x2)]} (0/0型极限,应用罗比达法则)
=e^{lim(x->+∞)[(-2/π)(1/(1+1/x2))]}
=e^[(-2/π)(1/(1+0))]
=e^(-2/π).
- 评论列表(网友评论仅供网友表达个人看法,并不表明本站同意其观点或证实其描述)
-
