已知函数f(x)=x2-4x-5，若在区间(-1，5)上，y=kx+3k的...

精选知识

当x∈（-1，5）时，f（x）=-x²+4x+5．
由y=y＝k(x+3)

y＝?2x

2

+4x+5

得x²+（k-4）x+（3k-5）=0．
令△=（k-4）²-4（3k-5）=0，解得 k=2或k=18，
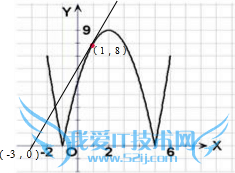
在区间（-1，5）上，当k=2时，y=2（x+3）的图象与函数f（x）的图象只交于一点（1，8）；
当k=18时，y=18（x+3）的图象与函数f（x）的图象没有交点．
如图可知，由于直线y=k（x+3）过点（-3，0），
当k＞2时，直线y=k（x+3）是由直线y=2（x+3）绕点（-3，0）逆时针方向旋转得到．
因此，在区间（-1，5）上，y=k（x+3）的图象位于函数f（x）图象的上方．
故k的取值范围为：（2，+∞）．

其他回答

应该是 K＞9/5把

其他类似问题

问题1：当k>2时,为什么 在区间【-1,5】上,y=kx+3k的图像位于函数F（x）= -x2+4x+5图像的上方?麻烦回答详细一点到最后一步,[数学科目]

设g(x)=kx+3k-F(x)=kx+3k+x²-4x-5=x²+(k-4)x+3k-5

若在区间[-1,5]上,y=kx+3k的图像位于函数F（x）= -x²+4x+5图像的上方

则在区间[-1,5]上,g(x)恒大于0

即g(x)=x²+(k-4)x+3k-5>0

当-(k-4)/26时,

g(x)的最小值为g(-1)=1-k+4+3k-5=2k>0

∴k>6时,g(x)≥g(-1)>0

当-1≤-(k-4)/22时,在区间[-1,5]上,g(x)>0

∴在区间[-1,5]上,y=kx+3k的图像位于函数F（x）= -x²+4x+5图像的上方

问题2：已知函数f(x)=/x^2-4x-5/,若在区间【-1,5】上,y=kx+3k的图像位于函数f(x)的上方,求k的取值范围.[数学科目]

∵f(x)=|x2-4x-5|=|(x+1)(x-5)|在区间【-1,5】上,

则f(x)=-(x+1)(x-5)=-x2+4x+5,-1≤x≤5

x轴=-b/2a=2,顶点为(2,9)

又y=kx+3k=k(x+3)是恒过点(-3,0)的直线

为满足y=kx+3k的图像位于函数f(x)的上方,先得找出直线与f(x)的临界情况

设f(x)与直线y=kx+3k在-1≤x≤5只有一个交点,设为切点(m,n)

对f(x)求导得y′=-2x+4=k

将k带入y=k(x+3)得

y=(-2x+4)(x+3)=-2x2-2x+12

则n=-m2+4m+5

n=-2m2-2m+12

联立上两式,解得m=1 (m=-7排除)

此时k=2

因此k的范围是k>2

问题3：已知函数f（x）=|x2-4x-5|，若在区间（-1，5）上，y=kx+3k的图象位于函数f（x）的上方，求k的取值范围．[数学科目]

当x∈（-1，5）时，f（x）=-x²+4x+5．
由y=y＝k(x+3)

y＝?2x

2

+4x+5

得x²+（k-4）x+（3k-5）=0．
令△=（k-4）²-4（3k-5）=0，解得 k=2或k=18，
在区间（-1，5）上，当k=2时，y=2（x+3）的图象与函数f（x）的图象只交于一点（1，8）；
当k=18时，y=18（x+3）的图象与函数f（x）的图象没有交点．
如图可知，由于直线y=k（x+3）过点（-3，0），
当k＞2时，直线y=k（x+3）是由直线y=2（x+3）绕点（-3，0）逆时针方向旋转得到．
因此，在区间（-1，5）上，y=k（x+3）的图象位于函数f（x）图象的上方．
故k的取值范围为：（2，+∞）．

问题4：要使函数y=kx+3k+1（-3＜x＜3）的图像上的点全在x轴上方,求实数k的取值范围[数学科目]

就是让y>0和-3＜x＜3代入方程就可以了!

可得k(x+3)+1>0

解得：当K＞0时,（-3k-1)/k

问题5：当k>2时,为什么 在区间【-1,5】上,y=kx+3k的图像位于函数F（x）= /-x2+4x+5/图像的上方?//为绝对值请问可不可以用多种方法来解,越简单越好,若要画图,请附上图,不要只写思路,[数学科目]

方法一：要一个个点的画图

x= -1,y=2k>4,F=0

x=0,y=3k>6,F=5

x= 1,y=4k>8,F=8

x= 2,y=5k>10,F=8

x= 3,y=6k>12,F=8

x= 4,y=7k>14,F=5

x= 5,y=8k>16,F=0

方法二：因为k>2,在区间【-1,5】

所以y是递增,最小值为y=2k>4,在x= -1处取得

因为F（x）= /-x2+4x+5/对称轴为2

所以为对称函数 最大值为8,在x=2处取得

因为当x= -1时,F=0小于y

当X=2时,y＞10大于F

即证