...且边长分别为2和3，在BG上截取GP=2，连结AP、PF.1、...

精选知识

1、图中,有△ABP≌△PGF(AB=PG=2,BP=FG=3,∠ABP=∠PGF=90°)

∴将△PGF向左平移5个单位,G和B重合,再将△PGF绕G(B)顺时针旋转90°,那么△ABP和△PGF重合

2、

其他回答

h固定方法法国的风格的水电费

追问： 汗、、、、、

其他类似问题

问题1：如图所示,正方形ABCD的边CD在正方形ECGF的边CE上,B.C.G三点在一条直线上,且边长分别速度啊 如图所示,正方形ABCD的边CD在正方形ECGF的边CE上,B.C.G三点在一条直线上,且边长分别为2和3,在BG上截取GP=[数学科目]

（1）AP⊥PF

对△ABP和△PGF来说,

AB=PG=2,BP=5-2=3=GF=3

∠P=∠G=90°

∴△ABP≌△PGF

∴∠BAP=∠GPF

∵∠BAP+∠BPA=90°

∴∠GPF+∠BPA=90°

∴∠APF=90°,即AP⊥PF

（2）△ABP≌△PGF

将△ABP平移令B点与△PGF的G点重合,然后以G为中心旋转△ABP90°,△ABP与△PGF即重合.

（3）将△ABP绕A点逆时针旋转至AB边与AD边重合,将△PGF绕F点顺时针旋转至FG与FE重合,即可得到大正方形.其中AP与FP为其两个边

知道AP=FP=√（2^2+3^2）=√13

故大正方形的周长为4√13

问题2：如图,正方形ABCD的边CD在正方形ECGF的边CE上,B、C、G三点在一条直线上,且边长分别为5和12.(1)连接AF、BE相较于M,求∠EMF度数并说明理由；(2)求AF和EM长度.老师PPT中的辅助线是这样，但没有过程，

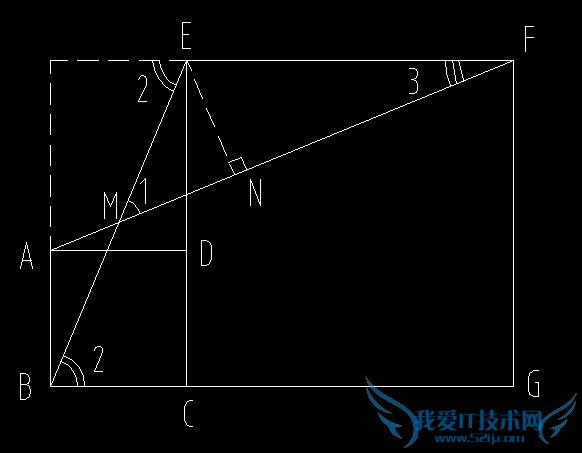
只说解题步骤,详细的内容你可以自己做：

按上图作辅助线.

∠2=∠3-∠1

∴tan∠2=tan（∠3-∠1）

=（tan∠3-tan∠1）/（1-tan∠3×tan∠1）

=.=1

所以,∠2=45°

EM=(√2)×EN

=(√2)×(EF×sin∠3）

=.

问题3：如图,正方形ABCD的边CD在正方形ECGF的边CE上,B,C,G三点共线,且边长分别为2cm和3cm,在BG有一动点P,沿着BG从B向G运动,速度为每秒1cm,连结AP PF AF.设运动时间是t秒,⑴则△APF的面积为＿＿＿＿＿＿（用t[数学科目]

（1）2×2+3×3-t-3/2·(5-t)=5.5+0.5t

（2）变大

（3）3

（4）3

莲子待青春 很高兴为您解答!

请放心使用,有问题的话请追问

采纳后你将获得5财富值.

你的采纳将是我继续努力帮助他人的最强动力!

问题4：（1）如图,正方形ABCD的边CD在正方形ECGF的边CE上,点B在GC的延长线上,连接BE,DG.BE与DG有怎么的关系,证明你的结论.（2）正方形ECGF位置保持不变,将正方形ABCD绕点C旋转,那么在旋转过程中,（1）中[数学科目]

1

因为 EBC GDC全等(SAS)

BE= GD

2

在旋转过程中

会发生变化

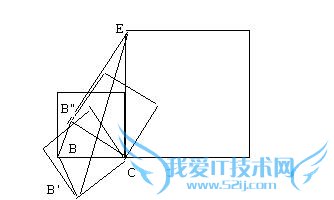
B'E 增大

B"E 减少

用余弦定理判断

设小正方形边长 a

大正方形边长 b

BE = c

BE' =c'

BE" =c"

在三角形EBC, EBC', EBC"中,

c2= a2+b2 -2ab cosC

c'2= a2+b2 -2ab cosC'

c"2= a2+b2 -2ab cosC"

C'cosC=0, c'2

C">C, cosC" c2. c">c

问题5：正方形ABCD的边CD在正方形ECGF的边CE上,BCD三点在一条直线上,边长分别为2,3.若把这个图形沿着PA,PF剪成三（1）观察猜想AP与PF之间的数量关系及位置关系,并说明理由.（2）图中是否存在通过旋转[数学科目]

（1）猜想PA=PF；

理由：∵正方形ABCD、正方形ECGF,

∴AB=BC=2,CG=FG=3,∠B=∠G=90°,

∵PG=2,

∴BP=2+3-2=3=FG,AB=PG,

∴△ABP≌△PGF,

∴PA=PF．

（2）存在,是△ABP和△PGF,

把△ABP先向右平移5个单位,使AB在GF边上,B与G重合,

再绕G点逆时针旋转90度,就可与△PGF重合．（答案不唯一）

（3）如图：

S大正方形的面积=S正方形ABCD的面积+S正方形ECGF的面积=4+9=13