余弦定理证明过程

精选知识

在任意△ABC中

做AD⊥BC.

∠C所对的边为c,∠B所对的边为b,∠A所对的边为a

则有BD=cosB*c,AD=sinB*c,DC=BC-BD=a-cosB*c

根据勾股定理可得：

AC^2=AD^2+DC^2

b^2=(sinB*c)^2+(a-cosB*c)^2

b^2=sin^2B*c^2+a^2+cos^2B*c^2-2ac*cosB

b^2=(sin^2B+cos^2B)*c^2-2ac*cosB+a^2

b^2=c^2+a^2-2ac*cosB

cosB=(c^2+a^2-b^2)/2ac

其他类似问题

问题1：求余弦定理的证明过程,配图.[数学科目]

平面向量证法

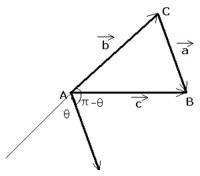
　　∵如图,有a+b=c (平行四边形定则：两个邻边之间的对角线代表两个邻边大小）

∴c·c=(a+b)·(a+b) 　　∴c^2=a·a+2a·b+b·b∴c^2=a^2+b^2+2|a||b|Cos(π-θ) 　　（以上粗体字符表示向量） 　　又∵Cos(π-θ)=-Cosθ 　　∴c^2=a^2+b^2-2|a||b|Cosθ（注意：这里用到了三角函数公式） 　　再拆开,得c^2=a^2+b^2-2*a*b*CosC 　　即 CosC=(a^2+b^2-c^2)/2*a*b 　　同理可证其他,而下面的CosC=(c^2-b^2-a^2)/2ab就是将CosC移到左边表示一下.

问题2：证明：余弦定理余弦定理证明方法[数学科目]

余弦定理是揭示三角形边角关系的重要定理,直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题,若对余弦定理加以变形并适当移于其它知识,则使用起来更为方便、灵活．

对于任意三角形 三边为a,b,c 三角为A,B,C 满足性质

a^2=b^2+c^2-2*b*c*CosA

b^2=a^2+c^2-2*a*c*CosB

c^2=a^2+b^2-2*a*b*CosC

CosC=(a^2+b^2-c^2)/2ab

CosB=(a^2+c^2-b^2)/2ac

CosA=(c^2+b^2-a^2)/2bc

证明：

如图：

∵a=b-c

∴a^2=(b-c)^2 （证明中前面所写的a,b,c皆为向量,^2为平方）拆开即a^2=b^2+c^2-2bc

再拆开,得a^2=b^2+c^2-2*b*c*CosA

同理可证其他,而下面的CosA=(c^2+b^2-a^2)/2bc就是将CosA移到右边表示一下.

---------------------------------------------------------------------------------------------------------------

平面几何证法：

在任意△ABC中

做AD⊥BC.

∠C所对的边为c,∠B所对的边为b,∠A所对的边为a

则有BD=cosB*c,AD=sinB*c,DC=BC-BD=a-cosB*c

根据勾股定理可得：

AC^2=AD^2+DC^2

b^2=(sinB*c)^2+(a-cosB*c)^2

b^2=sin^2B*c^2+a^2+cos^2B*c^2-2ac*cosB

b^2=(sin^2B+cos^2B)*c^2-2ac*cosB+a^2

b^2=c^2+a^2-2ac*cosB

cosB=(c^2+a^2-b^2)/2ac

从余弦定理和余弦函数的性质可以看出,

如果一个三角形两边的平方和等于第三

边的平方,那么第三边所对的角一定是直

角,如果小于第三边的平方,那么第三边所

对的角是钝角,如果大于第三边,那么第三边

所对的角是锐角.即,利用余弦定理,可以判断三角形形状.

同时,还可以用余弦定理求三角形边长取值范围.

这是百度上的,有些时候自己百度下就好了,

问题3：余弦定理的证明方法及过程[数学科目]

任意做三角形ABC,记BC=a,AC=b,AB=c,BC所对角为α,过B做BD⊥AC交AC于点D

则有两个直角三角形Rt△ABD与Rt△BDC

BD=csinα,AD=ccosα,CD=b-ccosα

由勾股定理,BD^2+CD^2=BC^2

(csinα)^2+(b-ccosα)^2=b^2-2bccosα+c^2[(sinα)^2+(cosα)^2]=b^2-2bccosα+c^2=a^2

即证余弦定理a^2=b^2+c^2-2bccosα

同理可证余弦定理其他式子

问题4：余弦定理的证明过程[数学科目]

△ABC 的 三边为 向量{ a,b,c},则 a-b=c 所以 （a-b）(a-b)= c c

由向量的点乘的意义得：a^2 +b^2 - 2ab= c^2

∴ a^2 +b^2 -2ab×cos（α）=c^2 （这里的 a b c 是向量的模）

问题5：如何证明余弦定理[数学科目]

可以参考一下：http://www.cbe21.com/subject/maths/html/040201/2001_01/20010109_311.html

用向量来证明是比较方便的.我们高一的课本上面就有,是新课标粤教版的第四册,其他的版本应该也都大同小异吧.

这个页面的中间部分有向量的证明方法：

http://www.pkuschool.com/zadmin/manage/details.asp?TopicAbb=directions&FileName=g1v4sxb5570a05.htm