一道九年级函数应用题 急小李推铅球 铅球运动过程中...

精选知识

1.

首先,水平距离一定要大于等于0 所以x>=0

其次,高度一定要大于等于0 所以 y>=0

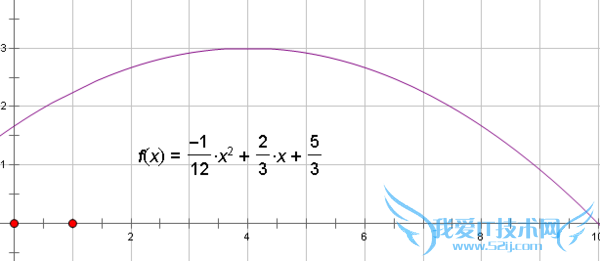
所以令 y=-1/12·x^2+2/3·x+5/3=0

也就是 -1/12(x^2-8x-20)=-1/12(x-10)(x+2)=0

所以x=10或-2(-2去掉,因为x>=0)

所以这个函数的定义域是 0<=x<=10

2.

2-1画出函数和y轴的交点 (0,5/3)

2-2画出函数的对称轴, x=4

2-3画出函数和x轴交点(10,0)

确定这3点之后就可以画出图像

3.

小李投球的距离函数已知,

令 y=0 得到x=10

所以小李的成绩是 10m

其他类似问题

问题1：有一座抛物线形拱桥，正常水位时，桥下水面宽度为20m，拱顶距水面4m． （1）如图所示的直角坐标系中，求出该抛物线的关系式．（2）在正常水位的基础上，当水位上升h（m）时，桥下水面[数学科目]

（1）设二次函数解析式为y=ax²，
代入点（10，-4）得-4=100a，
解得a=-125

，
因此二次函数解析式为y=-125

x²；
（2）把点（d2

，-4+h）代入函数解析式y=-125

x²，
得h=4-1100

d²；
（3）当桥下水面的宽度等于18m时，抛物线上第四象限点的横坐标为9，
把x=9代入函数解析式y=-125

x²中，
∴y=-125

×9²=-8125

（米），
∴4+2-8125

=6925

．
答：当水深超过6925

米时，超过了正常水位1925

，就会影响过往船只在桥下顺利航行．

问题2：一道九年级的二次函数的实际应用题某公园草坪的防护栏是由100段形状相同的抛物线形组成的．为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m（如图）[数学科目]

以这条防护栏的顶点所在铅直直线为y轴,防护栏底部所在直线为x轴建立直角坐标系；则

防护栏（抛物线）的顶点为（0,0.5）,还经过点（1,0）；

设防护栏所在的抛物线为y=ax2＋0.5,则a＋0.5＝1解得a＝﹣0.5

∴y＝﹣0.5x2＋0.5

当x＝±0.2时,y＝﹣0.5×﹙±0.2﹚2＋0.5＝0.5×﹙1－0.04﹚＝0.48

当x＝±0.6时,y＝﹣0.5×﹙±0.6﹚2＋0.5＝0.5×﹙1－0.36﹚＝0.32

∴这条防护栏需要不锈钢支柱的总长度至少为﹙0.48＋0.32﹚×2＝1.6m.

问题3：一道函数应用题某商品在最近100天内的价格f(t)与时间t的函数关系式是t/4+22 (0≤t≤40,t属于N*)f(t)= -t/2+52 (40[数学科目]

设销售额是y=f(t)*g(t)

0

问题4：一个矩形养鸡场由一堵旧墙（旧墙的长度不小于l米）和总长为l米的篱笆围成,中间篱笆把分割成两个小矩形,设大矩形的垂直于旧墙的一边长为x米,面积为s平方米,求s关于x的函数解析式,并写[数学科目]

大矩形的长为l-3x

s=长*宽=x(l-3x)

由0

问题5：九年级二次函数应用题1.已知二次函数y=x的平方+bx+c中,函数y与自变量x的部分对应值如下：X … -1 0 1 2 3 4 …y … 10 5 2 1 2 5 …(1) 、求该二次函数的关系式；(2) 、当x为何值时,y有最小值?最小值

1.y=x^2-4x+5

x=2时,y=1

当m≤1时,y1≥y2；当m≥1时,y1≤y2

2.实在没图解不出来,你自己随便写一下吧.

记得把分给我.