...7点到8点在某地会面，先到者等侯另一方20分钟，过时...

精选知识

设两人约会时长为A,双方等待时长为B,将约会时长分为N个时刻,则双方到达约会地的时该排列总数为N*N（题中式1）

双方若要相遇,则先后到达约会的时刻差要小于或等于等待时刻数（B/A*N）（题中式2）这可分为以下情况：

双方同时到达：排列数为N

双方差一刻到达：排列数为（N-1）*2

双方差两刻到达,排列数为（N-2）*2

……

双方差B/A*N到达,排列数为（N-B/A*N）*2

以上各种情况排列数之和为（N-1+N-B/A*N）*B/A*N+N

两人相遇的概率={（N-1+N-B/A*N）*B/A*N+N}/N*N

求上式N趋于无穷大时的极限为2（B/A）-（B/A）^2={A^2-(A-B)^2}/A^2

题中式3中的40就是A-B=40

这类概率题,假设双方等候时长和约会时长之比为A,则相遇概率为2A-A*A

如约会时长为一小时,等候时长为半小时,则其A=1/2

概率=2*1/2-1/4=3/4

如果等待时间和约会时间一样长（这样就是不见不散了）,则A=1,概率为1.

以上推导若有疑问,请复习排列组合、等差数列求各公式及极限算法.

也可用面积的概念来说明：

画X为横座标,Y为纵座标的直角坐标系,事件的集合即为在坐标系中的正方形（边长为60,面积为3600）,如双方没见面,即有Y>X+20 Y

其他类似问题

问题1：甲乙两人相约在7点到8点之间在某地会面,先到者等候20分钟即可离去,设两人在指定的甲乙两人相约在7点到8点之间在某地会面，先到者等候20分钟即可离去，设两人在指定的一小时内任意时刻[数学科目]

40/60=2/3

假设甲在某一时间点到达,乙只要在这个点前后各20分钟内到达就可以会面,也就是说乙和甲会面的概率就是2*20/60

问题2：两人相约在7点到8点在某地会面，先到者等候另一个人20分钟方可离去．试求这两人能会面的概率？[数学科目]

以X、Y分别表示两人到达时刻，建立直角坐标系如图：
则0≤X≤60，0≤Y≤60．两人能会面的充要条件是|X-Y|≤20
∴P=

S

阴

S

OABC

＝

60

2

?(60?20

)

2

60

2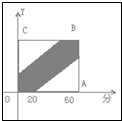

＝59

问题3：两人相约在7点到8点在某地会面，先到者等候另一个人20分钟方可离去．试求这两人能会面的概率？[数学科目]

以X、Y分别表示两人到达时刻，建立直角坐标系如图：
则0≤X≤60，0≤Y≤60．两人能会面的充要条件是|X-Y|≤20
∴P=

S

阴

S

OABC

＝

60

2

?(60?20

)

2

60

2

＝59

问题4：两人相约8点到9点在某地会面,先到者等候另一人20分钟,过时就可离去.问：那么这两人能见面的机会有多大能会面的点的区域用阴影标出的图也献上[数学科目]

设先到者到达时间是8点后x分,后到者到达时间是8点后y分

则有：x∈[0,60],y∈[0,60],且 x≥y.

要是两人相遇,后到者需在先到者到达20分钟之内到达即 y≤x+20.

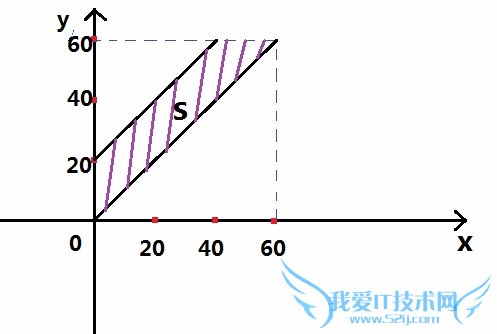
则有：x≤y≤x+20,x,y属于[0,60],表示如图

则S区域中的x,y组合意味两人可以相遇

P=P(x,y∈S)=S区域面积/x,y∈[0,60]区域面积

=(20*40+20*20*0.5) / (60*60)=5/18

问题5：两人相约在7点到8点在某地会面，先到者等候另一个人20分钟方可离去．试求这两人能会面的概率？

以X、Y分别表示两人到达时刻，建立直角坐标系如图：
则0≤X≤60，0≤Y≤60．两人能会面的充要条件是|X-Y|≤20
∴P=

S

阴

S

OABC

＝

60

2

?(60?20

)

2

60

2

＝59