欢迎您访问52IJ教育培训网,今天小编为你分享的数学方面的学习知识是通过网络精心收集整理的:“手打吧_...3,5.第六题的1,2为什么不能图片。手打吧~求下列函...[数学]”,注意:所整理内容不代表本站观点,如你有补充或疑问请在正文下方的评论处发表。下面是详细内容。
(1)dz/dx=3x^2y-y^3 dz/dy=x^3-3xy^2
d2z/dx2=3xy,d2z/dy2=-3xy,d2z/dxdy=3x^2-3y^2
2)t=xy dt/dx=y;dt/dy=x;d2t/dx2=0;d2t/dy2=0;d2t/dxdy=1
dz/dt=0.5*(lnt)^(-0.5)/t=1/[ 2sqrt(lnt)*t ]
d2z/dt2=-0.5(lnt)^(-0.5)*t^(-2)-0.25(lnt)^(-1.5)*t(-2)= - (2lnt+1) / { 4 * [ sqrt(lnt)^3] * t^2 }
dz/dx=dz/dt*dt/dx; dz/dy=dz/dt*dt/dx
d2z/dx2=d2z/d2t*(dt/dx)^2+dz/dt *d2t/dx2= - (2lnt+1) / { 4 * [ sqrt(lnt)^3] * t^2 } *y^2+ *0
= - (2lnxy+1) / { 4 * [ sqrt(lnxy)^3] * x^2 }
对称性d2z/dy2=- (2lnxy+1) / { 4 * [ sqrt(lnxy)^3] * y^2 }
d2z/dxdy=d(dz/dt*dt/dx)/dy=d2z/dt2*dt/dx*dtdy+dz/dt*d2t/dxdy=
- (2lnxy+1) / { 4 * [ sqrt(lnxy)^3] * t^2 }*x*y+1/[ 2sqrt(lnt)*t ]*1
=(2lnt-1)/ [4 * [ sqrt(lnxy)^3] * t]=(2lnxy-1) / [4 * [ sqrt(lnxy)^3] * t]
其他类似问题
问题1:函数连续,函数可微,函数可导,偏导数存在,偏导数连续之间的关系,最好有例子证明,函数可微为什么在这些关系中最强?[数学科目]
对于一元函数
函数连续 不一定 可导 如y=|x|
可导 一定 连续 即连续是可导的必要不充分条件
函数可导必然可微
可微必可导 即可导是可微的必要充分条件
对于多元函数
偏函数存在不能保证该函数连续 如 xy/(x^2+y^2) x^2+y^2不等于0
(不同于一元函数) z= f(x,y)=
0 x^2+y^2=0
函数连续当然不能推出偏导数存在 由一元函数就知道
问题2:高数 2元函数求偏导数xyz+(x^2+y^2+z^2)^(1/2)=2^(1/2) 两边分别对x,y求偏导数[数学科目]
对x偏导的时候,就把y,z看成是常数;
同样偏导y的时候把x,z当成是常数;
对z偏导的时候,把x,y当成是常数.
应该不难了吧?
问题3:一道高数题,求此函数的偏导数,(1)z=lnctg(x/y)(2)设Z^3-3xyz=a^2,求d^2z/dxdy(d是偏导数的符号)[数学科目]
1.先对x求偏导:把y看做常量,用复合函数求导法来算(因为偏导的符号打不出,省略一下)
- 1/ctg(x/y) * csc^2(x/y) * 1/y
再对y求偏导,把 x看做常量
1/ctg(x/y) * csc^2(x/y) *(x/y^2)
2.和第一题方法是一样的.先对x偏导,得出一个式子,在这个式子里对y偏导.你自己练习一下吧,光看答案是没用的.
问题4:高数中多元函数偏导数这个定理怎么用啊?如何判断二阶混合偏导数连续啊?这个定理的前提是要知道两个二阶偏导数连续,因为只有先求出这两个偏导数才能证明它俩是否连续,既然两个偏导数[数学科目]
考研试卷中的都连续 你就大胆的用吧 这个没有问题的
这个定理主要是用在求二阶偏导的时候交换一下顺序,可能会有柳暗花明又一村的感觉
问题5:一道费解的高数问题 (多元函数,偏导数)设u=f(x+y+z,x^2+y^2+z^2),其中f有二阶连续偏导数,求Δu= ?平方u/ ?x平方+?平方u/ ?y平方+?平方u/ ?z平方?[数学科目]
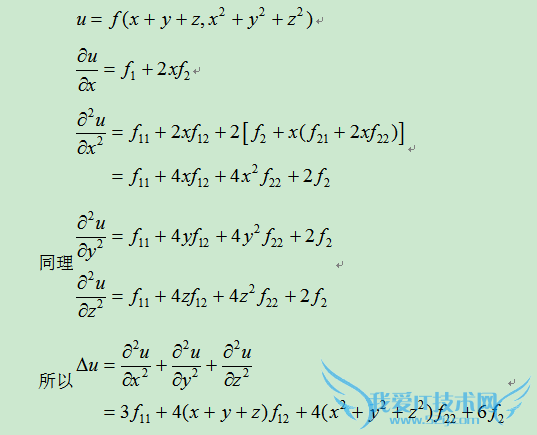
- 评论列表(网友评论仅供网友表达个人看法,并不表明本站同意其观点或证实其描述)
-
