一道概率论于数理统计题这个答案是怎么算出来的

精选知识

第一个是查表得到的,一般概率论的书后面都有一张标准正态分布表,类似这个

u0.05是指标准正态分布下,大于u0.05的概率等于0.05的那个值

也就是说不超过u0.05的概率等于0.95

可以看到表中第一列为1.6,第一行为0.04对应的值是0.9495,表中第一列为1.6,第一行为0.05对应的值是0.9505,也就是u0.0505=1.64,u0.04955=1.65

一般就大致的取个平均,得到u0.05=1.645

其他回答

这是分位数的意思，表示在标准正态分布中，大于1.645的数占整体的0.05（即5%）

一般通过查表得到

其他类似问题

问题1：数学:概率论与数理统计盒中装有大小相等的球10个,编号分别为0`1`2……9,从中任取1个,观察号码是“小于5”`“等于5”`“大于5”的情况.试定义一个随机变量,求其分布律和分布函数."步骤"尽

先来求各种情况的概率

小于5的情况有 0,1,2,3,4 共5种

等于5的情况有 5 共1种

大于5的情况有 6,7,8,9 共4种

所有情况是 0,1,2,3,4,5,6,7,8,9 共10种

所求各概率等于 满足条件的情况数/总情况数

于是P{摸到球的编号小于5}=5/10=1/2

P{摸到球的编号等于5}=1/10

P{摸到球的编号大于5}=4/10=2/5

取一个随机变量X

分别用 X=-1表示 P{摸到球的编号小于5}

X=0 表示 P{摸到球的编号等于5}

X=1 表示 P{摸到球的编号大于5}

于是列出X的分布律,这里采用表格法

X= -1 0 1

P= 1/2 1/10 2/5

这就是所求的分布律啦!

下面还要求分布函数F(X)

根据分布律的表格很容易写出分布函数

因为是离散点,所以用分段函数来表示

只要把各段的函数值和对应的定义域分别写出即可注意,分布函数和分布律有不同,分布函数可以说是不同分段的分布律的累加.

因为分布律可以通过分布函数取不同点的值想减得到.

0 x∈（-∞,-1)

F(X)= 1/2 x∈[-1,0)

3/5 x∈[0,1)

1 x∈[1,+∞)

当x∈[0,1)时,F(X)=1/2+1/10=3/5

这里就是累加了分布律的两个取值区间.

同理 x∈[1,+∞)时,3/5+2/5=1 也是累加.

问题2：某人有n把钥匙,其中只有一把能打开门,现从中任取一把试开,试过的不再重复,直至把门打开为止,求试开次数的数学期望和方差.[数学科目]

设随机变量代表到打开为止时的开门次数,则

P(X=m) = (n-1)/n .(n-2)/(n-1) ...1/(n-m+1) = 1/n

其中 m=1,2...,n

因此

E(X) = 1*(1/n) + 2*(1/n) + ...+ n*(1/n) = (1+2+...+n) * (1/n) = (1+n)/2

E(X^2) = (1^2)*(1/n) + (2^2)*(1/n) + ...+ (n^2)*(1/n)

= (1^2+2^2+...+n^2) * (1/n)

= n(n+1)(2n+1)/6 * (1/n) = (n+1)(2n+1)/6

V(X) = E(X^2) - [E(X)]^2 = (n+1)(2n+1)/6 - (1+n)^2/4 = （这个式子的化简请自己算 :P）

问题3：概率论与数理统计,第二个题! [数学科目]

<=2,分析如图,

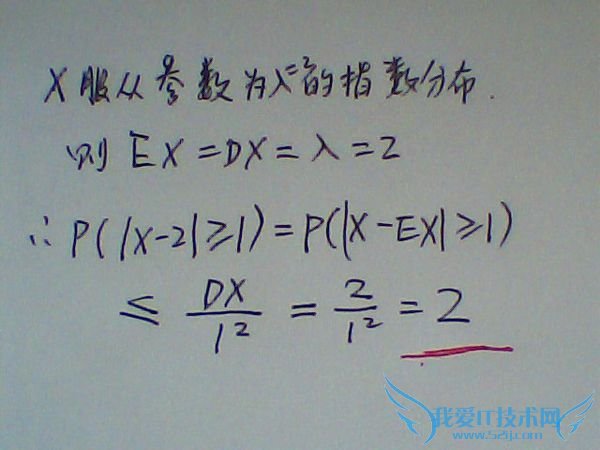
问题4：概率论与数理统计 [数学科目]

由于ABC三个时间是任意的.根据相互独立事件有P(AB)=P(A)P(B),故

P(AB)+P(AC)-(BC)=P(AB)+P(C)*(P(A)-P(B))<=P(AB)+P(A)-P(B)=P(A)+P(B)*(P(A)-1)<=P(A)

当且仅当P(C)=P(A)=1时,“=”成立

问题5：一道关于概率论与数理统计的题X是服从参数为λ的泊松分布.且已知E[(X2-3X+2)]=1,则λ=?[数学科目]

E[(X2-3X+2)]=1

泊松分布以期望、方差均等于参数为数字特征：E(X)=D(X)=λ

而由方差D(X)=E（X^2）-E(X)^2,

可得E（X^2）=λ+λ^2

于是,

E[(X^2-3X+2)]=E（X^2）-3E(X)+2=λ+λ^2-3λ+2=1

即λ^2-2λ+1=0

解得λ=1