2014数学中考徐州最后一题答案28. (本题10分)如图，矩...

精选知识

分析：

（1）只要证到三个内角等于90°即可．
（2）易证点D在⊙O上,根据圆周角定理可得∠FCE=∠FDE,从而证到△CFE∽△DAB,根据相似三角形的性质可得到S矩形ABCD=2S△CFE=[(

3CF)^2]/4．然后只需求出CF的范围就可求出S矩形ABCD的范围．根据圆周角定理和矩形的性质可证到∠GDC=∠FDE=定值,从而得到点G的移动的路线是线段,只需找到点G的起点与终点,求出该线段的长度即可．

（1）证明：如图1,
∵CE为⊙O的直径,
∴∠CFE=∠CGE=90°．
∵EG⊥EF,
∴∠FEG=90°．
∴∠CFE=∠CGE=∠FEG=90°．
∴四边形EFCG是矩形．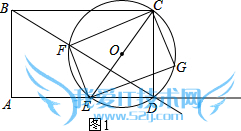

（2）①存在．
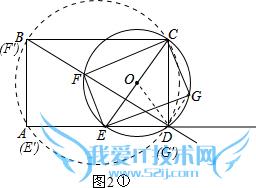
连接OD,如图2①,
∵四边形ABCD是矩形,
∴∠A=∠ADC=90°．
∵点O是CE的中点,
∴OD=OC．
∴点D在⊙O上．
∵∠FCE=∠FDE,∠A=∠CFE=90°,
∴△CFE∽△DAB．

∴S△CFE/S△DAB=（CF/DA）^2．

∵AD=4,AB=3,
∴BD=5,
S△CFE=（CF/4）^2?S△DAB=CF^2/16×1/2×3×4=[(3CF)^2]/8．

∴S矩形ABCD=2S△CFE=[(3CF)^2]/4．

∵四边形EFCG是矩形,
∴FC∥EG．
∴∠FCE=∠CEG．
∵∠GDC=∠CEG,∠FCE=∠FDE,
∴∠GDC=∠FDE．
∵∠FDE+∠CDB=90°,
∴∠GDC+∠CDB=90°．
∴∠GDB=90°
Ⅰ．当点E在点A（E′）处时,点F在点B（F′）处,点G在点D（G′处,如图2①所示．）

此时,CF=CB=4．
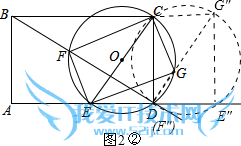
Ⅱ．当点F在点D（F″）处时,直径F″G″⊥BD,
如图2②所示,
此时⊙O与射线BD相切,CF=CD=3．
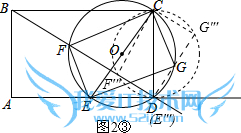
Ⅲ．当CF⊥BD时,CF最小,此时点F到达F″′,
如图2③所示．
S△BCD=1/2BC?CD=1/2BD?CF″′．

∴4×3=5×CF″′．
∴CF″′=12/5．

∴12/5≤CF≤4．

∵S矩形ABCD=[(3CF)^2]/4,

∴3/4×（12/5）^2≤S矩形ABCD≤[3/4]×4^2．

∴108/25≤S矩形ABCD≤12．

∴矩形EFCG的面积最大值为12,最小值为108/25．

②∵∠GDC=∠FDE=定值,点G的起点为D,终点为G″,
∴点G的移动路线是线段DG″．
∵∠GDC=∠FDE,∠DCG″=∠A=90°,
∴△DCG″∽△DAB．
∴DC/DA=DG″/DB．

∴3/4=DG″/5．

∴DG″=15/4．

∴点G移动路线的长为15/4．

其他类似问题

问题1：舟山定海区2014中考题,求详解.现在很多家庭都使用折叠型西餐桌来节省空间,两边翻开后成圆形桌面(如图1)．餐桌两边AD和BC平行且相等(如图2),小华用 皮带尺量出AC=1.2米,AB=0.6米, 那么桌面翻成[数学科目]

取AC中点E,连接BE,由题意得：AC=2AB,E为中点,所以三角形ABE为正三角形,所以角AEB=2角ACB,由用一段弧所对应的2圆周角=圆心角,所以圆直径为AC,半径=0.6,所以面积=2*60/360*π*0.6^2-2*1/2*0.6*0.3根号3

问题2：2010江苏徐州数学中考压轴题[数学科目]

　　（江苏省徐州市）如图,已知二次函数y＝－ x 2＋ x＋4的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC．

　　（1）点A的坐标为____________,点C的坐标为____________；

　　（2）线段AC上是否存在点E,使得△EDC为等腰三角形?若存在,求出所有符合条件的点E的坐标；若不存在,请说明理由；

　　（3）点P为x轴上方的抛物线上的一个动点,连接PA、PC,若所得△PAC的面积为S,则S取何值时,相应的点P有且只有两个,并求出此时点P的坐标．

　　（1）A（0,4）,C（8,0） 2分

　　（2）存在

　　设直线AC的解析式为y＝kx＋b

　　则b＝48k＋b＝0 解得k＝－ b＝4

　　∴直线AC的解析式为y＝－ x＋4 3分

　　∵抛物线的对称轴为x＝－ ＝3,∴D（3,0）

　　∴AD＝ ＝5,DC＝8－3＝5,∴AD＝DC

　　①当DE＝DC时,点E与点A重合,∴E1（0,4）

　　4分

　　②当EC＝DC时,则EC＝5,又AC＝ ＝

　　如图①,过E作EF⊥DC于F,则△EFC∽△AOC

　　∴ ＝ ,即 ＝ ,∴EF＝ ,∴FC＝

　　由－ x＋4＝ 得x＝8－

　　∴E2（8－ , ） 5分

　　③当ED＝EC时,如图①,过E作EG⊥DC于G,则DG＝ DC＝

　　∴OG＝OD＋DG＝3＋ ＝ ,代入y＝－ x＋4,得y＝

　　∴E3（ , ） 6分

　　综上所述,符合条件的点E有三个：E1（0,4）,E2（8－ , ）,E3（ , ）

　　（3）方法1：如图②,过P作PH⊥OC,垂足为H,交直线AC于点Q

　　设P（m,－ m 2＋ m＋4）,则Q（ ,－ m＋4）

　　①当0＜m＜8时

　　PQ＝(－ m 2＋ m＋4)－(－ m＋4)＝－ m 2＋2m

　　S△PAC ＝S△APQ ＋ S△CPQ ＝ ×8×(－ m 2＋2m)＝－(m－4)2＋16

　　∴0＜S≤16 7分

　　②当－2＜m＜0时

　　PQ＝(－ m＋4)－(－ m 2＋ m＋4)＝ m 2－2m

　　S△PAC ＝S△CPQ － S△APQ ＝ ×8×( m 2－2m)＝(m－4)2－16

　　∴0＜S＜20

　　故S＝16时,相应的点P有且只有两个 8分

　　当m＝4时,S＝16,此时y＝－ m 2＋ m＋4＝6

　　∴P1（4,6） 9分

　　由(m－4)2－16＝16,得m1＝4＋ （舍去）,m2＝4－

　　∴y＝－ m 2＋ m＋4＝ －2

　　∴P2（4－ , －2） 10分

　　方法2：如图③,将线段AC向上平移,记平移后的线段为A′C′,在A′C′与抛物线相切前,A′C′ 与抛物线始终有两个交点,加上线段AC下方的一个点,共有三个P点可以构成△PAC；当A′C′ 与抛物线相切时,满足条件的点P有且只有两个．

　　设直线A′C′ 的解析式为y＝－ x＋b,代入抛物线的解析式得：

　　－ x 2＋ x＋4＝－ x＋b,整理得：x 2－8x＋4b－16＝0

　　当A′C′ 与抛物线只有一个交点时,Δ＝(－8)2－4(4b－16)＝0

　　解得b＝8,∴A′A＝AO＝4

　　又∵A′C′‖AC,∴△PAC和△AOC的公共边AC上的高也相等

　　∴S△PAC ＝S△AOC ＝ ×8×4＝16

　　故当S＝16时,相应的点P有且只有两个 8分

　　联立y＝－ x＋8y＝－ x 2＋ x＋4 解得x＝4y＝6

　　∴P1（4,6） 9分

　　将线段AC向下平移至经过原点O,并向上延长交抛物线于点P2,

　　则S△P2AC ＝S△P1AC ＝S△AOC ＝16,直线OP2的解析式为y＝－ x

　　把y＝－ x代入y＝－ x 2＋ x＋4,得－ x 2＋ x＋4＝－ x

　　解得x1＝4＋ （舍去）,x2＝4－ ,∴y＝ －2

　　∴P2（4－ , －2） 10分