2011重庆市中考数学题如图所示：在平面直角坐标系xOy...

精选知识

（1）,作AD⊥x轴∵AO=5,tan∠AOE=4/3∴在 Rt△ADO中 AD/OD=4/3∴设AD为4x,则OD为3x∴在Rt△ADO AO2=AD2+OD2即52=（4x）2+（3x)2 25=16x2+9x2 25=25x2 x2=1∴x1=1,x2=-1（不和题意,舍去）∴OD=3,AD=4∴A（3,4）设反比例函数的解析式为y=k/x把A（3,4)代入反比例函数的解析式得：4=k/3 k=12∴反比例函数的解析式为y=12/x（2）,∵B（-6,n）把B点代入反比例函数的解析式得：n=-2∴B（-6,-2）设AB解析式为y=kx+b把A（3,4）,B（-6,-2）代入AB解析式得k=2/3,b=2∴AB解析式为y=2/3x+2设AB解析式交y轴于E点把x=0代入AB解析式得：y=2∴E（0,2）作AF⊥y轴,BG⊥x轴,BH⊥y轴∴有矩形AFOD∴AF=OD=3∴S△AEO=1/2*OE*AF=1/2*2*3=3∵B（-6,-2）∴BH=6,BG=2把y=0代入AB解析式得：x=3∴C（-3,0）,CO=3∴S△BOC=1/2*CO*BG=1/2*3*2=3∵CO=3,EO=2∴S△COE=1/2*CO*OE=1/2*3*2=3∴S△AOB=S△AEO+S△COE+S△BOC=3+3+3=9

其他类似问题

问题1：（2010,重庆）如图,在平面直角坐标系XOY中,直线AB与X轴交与点A（-2,0）,与反比例函数在第一象限内的图交与点B（2,N）,连接BO,若S三角形AOB=4.（1）求该比例函数的解析式和直线AB的解析式[数学科目]

：（1）由A（-2,0）,得OA=2；

∵点B（2,n）在第一象限内,S△AOB=4,

∴ OA?n=4；

∴n=4；（2分）

∴点B的坐标是（2,4）；（3分）

设该反比例函数的解析式为y= （a≠0）,

将点B的坐标代入,得4= ,

∴a=8；（4分）

∴反比例函数的解析式为：y= ；（5分）

设直线AB的解析式为y=kx+b（k≠0）,

将点A,B的坐标分别代入,得 ,（6分）

解得 ；

∴直线AB的解析式为y=x+2．（8分）

（2）在y=x+2中,令x=0,得y=2．

∴点C的坐标是（0,2）,∴OC=2；（9分）

∴S△OCB= OC×xB= ×2×2=2．

问题2：如图,在平面直角坐标系中一次函数y=-1/2x+6的图像分别交x,y轴于点a.b,与一次函数y=x的图像交于第一象内的点c.1.求a.b.c.的坐标 2.求三角形obc的面积.[数学科目]

一：

∵y=-1/2x+6的图像分别交x,y轴于点a、b

.∴a、b坐标分别为（12,0）、（0,6）

∵y=-1/2x+6与一次函数y=x的图像交于第一象限内的c点

∴-1/2x+6=x,解得X=4 ∴ C点坐标为（4,4）

二：

三角形obc的面积=?ob×oc=?×6×4=12

【知识点】：求两函数的交点坐标,只要联立解方程组即可.

如题中的y=-1/2x+6与一次函数y=x的图像交于第一象限内的c点的坐标详细解法为：

方程1：y=-1/2x+6

方程2：y=x C点是交点,两函数都经过此点, 即C点坐标既要满足方程1也要满足方程2.

∴-1/2x+6=x ∴x=4 C点坐标为（4,4）.

问题3：在平面直角坐标系xOy中，已知一次函数y=kx+b（k≠0）的图象过点P（1，1），与x轴交于点A，与y轴交于点B，且OAOB＝3，那么点A的坐标是______．[数学科目]

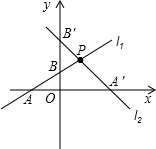令x=0，则y=b； 令y=0，则x=-bk

．
所以A（-bk

，0），B（0，b）．
∵一次函数y=kx+b（k≠0）的图象过点P（1，1），
∴k+b=1．
①若直线在l₁位置，则OA=bk

，OB=b．
根据题意有OAOB

=bkb

=1k

=3，∴k=13

．
∴b=1-13

=23

．
∴A点坐标为A（-2，0）；
②若直线在l₂位置，则OA=-bk

，OB=b
．根据题意有-1k

=3，∴k=-13

．
∴b=1-（-13

）=43

．
∴A点坐标为A（4，0）．
故答案为（-2，0）或（4，0）．

问题4：陕西的2013中考数学的24题怎么做啊!在平面直角坐标系中,一个二次函数的图象经过点A（1,0）在平面直角坐标系中,一个二次函数的图象经过点A（1,0）、B（3,0）两点．（1）写出这个二次函数图[数学科目]

呵呵http://www.qiujieda.com/math/9020957,我的答案啦

问题5：在平面直角坐标系xOy中，已知一次函数y=kx+b（k≠0）的图象过点P（1，1），与x轴交于点A，与y轴交于点B，且tan∠ABO=3，那么点A的坐标是______．[数学科目]

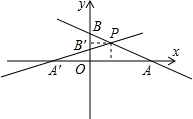在Rt△AOB中，由tan∠ABO=3，可得OA=3OB，则一次函数y=kx+b中k=±13

．
∵一次函数y=kx+b（k≠0）的图象过点P（1，1），
∴当k=13

时，求可得b=23

；
k=-13

时，求可得b=43

．
即一次函数的解析式为y=13

x+23

或y=-13

x+43

．
令y=0，则x=-2或4，
∴点A的坐标是（-2，0）或（4，0）．
故答案为：（-2，0）或（4，0）．